题目内容
5.已知a>0,集合A={x||x+2|<a},B={x|ax>1},若A∩B≠∅,则实数a的取值范围是(0,1)∪(2,+∞).分析 先求出A,再分a>1 和0<a<1两种情况,分别求得B,并根据A∩B≠∅,分别求得a的范围,综合可得结论.
解答 解:∵a>0,集合A={x丨丨x+2丨<a}={x|-a<x+2<a}={x|-a-2<x<a-2},
当a>1时,B={x丨ax>1}={x|x>0},
若A∩B≠∅,则有 a-2>0,解得a>2.
当0<a<1时,B={x|x<0},
若A∩B≠∅,则有-a-2<0,∴a>-2,故有 0<a<1.
综上可得,实数a的取值范围是(0,1)∪(2,+∞).
故答案为:(0,1)∪(2,+∞).
点评 本题主要考查绝对值不等式的解法,指数不等式的解法,集合间的包含关系,求集合中参数的取值范围,是中档题,解题时要注意分类讨论思想的合理运用.

练习册系列答案
相关题目
16.化简$\frac{{x}^{2}{x}^{-3}{x}^{\frac{2}{3}}}{{x}^{\frac{1}{3}}{x}^{-2}{x}^{-\frac{8}{3}}}$的结果是 ( )
| A. | x${\;}^{\frac{4}{3}}$ | B. | x2 | C. | x3 | D. | x4 |
10.已知函数f(x)=$\frac{\sqrt{1-{x}^{2}}}{|x-4|+|x+3|}$,则f(x)的图象关于( )
| A. | x轴对称 | B. | y轴对称 | C. | 原点对称 | D. | 直线y=x对称 |
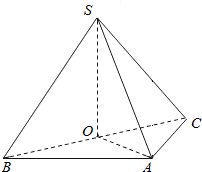 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°.