题目内容
已知可导函数
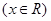 满足
满足 ,则当
,则当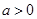 时,
时, 和
和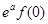 的大小关系为( )
的大小关系为( )
(A)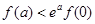 (B)
(B)
(C)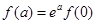 (C)
(C)
B
解析试题分析:根据题意,由于可导函数
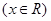 满足
满足 ,,则说明函数函数f(x)=
,,则说明函数函数f(x)=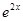 满足条件,那么可知f’(x)=2
满足条件,那么可知f’(x)=2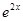 >f(x),因此比较f(0)=1,
>f(x),因此比较f(0)=1, f(0)=
f(0)=  ,而f(a)=
,而f(a)=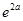 ,自然得到为
,自然得到为 ,选B.
,选B.
考点:复合函数的导数
点评:本题考查求复合函数的导数的方法,以及指数函数的单调性,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数 及其导函数
及其导函数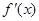 都是定义在R上的函数,则“
都是定义在R上的函数,则“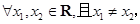
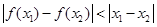 ”是“
”是“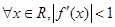 ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
曲线 在
在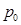 处的切线平行于直线
处的切线平行于直线 ,则
,则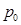 点的坐标为( )
点的坐标为( )
A.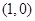 | B.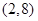 |
C.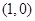 和 和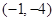 | D.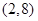 和 和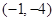 |
已知函数f(x)=x2+2x+blnx,若函数f(x)在(0,1)上单调,则实数b的取值范围是
| A.b≥ 0 | B.b<-4 | C.b≥0或b≤-4 | D.b>0或b<-4 |
函数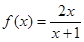 在[1,2]的最大值和最小值分别是 ( )
在[1,2]的最大值和最小值分别是 ( )
A.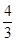 ,1 ,1 | B.1,0 | C.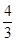 , ,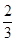 | D.1,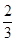 |
已知函数 则
则 的值为 ( )
的值为 ( )
| A.-20 | B.-10 | C.10 | D.20 |
若曲线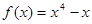 在点P处的切线平行于直线
在点P处的切线平行于直线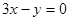 ,则点P的坐标为 ( )
,则点P的坐标为 ( )
| A.(1,0) | B.(1,5) | C.(1,-3) | D.(-1,2) |
设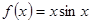 ,
,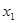 、
、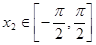 ,且
,且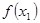 >
>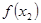 ,则下列结论必成立的是( )
,则下列结论必成立的是( )
A.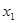 > >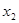 | B.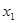 + +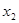 >0 >0 | C.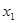 < <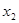 | D.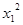 > > |
定义在R上的可导函数f(x),且f(x)图像连续,当x≠0时, 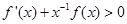 ,则函数
,则函数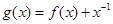 的零点的个数为( )
的零点的个数为( )
| A.1 | B.2 | C.0 | D.0或2 |