题目内容
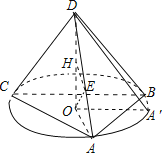
【题目】如图,已知四面体ABCD中,DA=DB=DC=![]() 且DA、DB、DC两两互相垂直,点
且DA、DB、DC两两互相垂直,点![]() 是△ABC的中心.
是△ABC的中心.

(1)求直线DA与平面ABC所成角的大小(用反三角函数表示);
(2)过![]() 作OE⊥AD,垂足为E,求ΔDEO绕直线DO旋转一周所形成的几何体的体积;
作OE⊥AD,垂足为E,求ΔDEO绕直线DO旋转一周所形成的几何体的体积;
(3)将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与直线BC所成角记为![]() ,求
,求![]() 的取值范图.
的取值范图.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)[0,
;(3)[0,![]() ].
].
【解析】
(1)由题意知可得![]() 即为直线DA与平面ABC所成角,在直角三角形DAO中求解即可.
即为直线DA与平面ABC所成角,在直角三角形DAO中求解即可.
(2)由圆锥的几何特征可得,该几何体由两个底面相等的圆锥组合而成,其中两个圆锥的高的和为![]() ,底为
,底为![]() ,代入圆锥的体积公式,即可得到答案;
,代入圆锥的体积公式,即可得到答案;
(3)根据异面直线所成角的定义,可得当直线DA与直线BC垂直时它们的所成角是90°,达到最大值.由直线与平面所成角的性质,当点A满足直线BC与OA平行时,直线DA与直线BC所成角等于∠OAD,达到最小值.由此结合题中数据加以计算,即可得到DA与BC所成角的余弦值的取值范围.
(1)由题意知,DO⊥底面ABC,∴![]() 即为直线DA与平面ABC所成角,
即为直线DA与平面ABC所成角,
∵DA=DB=DC=![]() 且DA、DB、DC两两互相垂直,∴AB=CB=AC=6,∴AO=
且DA、DB、DC两两互相垂直,∴AB=CB=AC=6,∴AO=![]()
∴![]()
![]() ,∴
,∴![]() .
.
(2)过E作EH⊥DO,由已知可得![]() ,
,![]() ,OE=2,由此得
,OE=2,由此得![]() ,
,
∴△DEO绕直线DO旋转一周所形成的几何体的体积![]() ;
;
(3)根据题意,可得在旋转过程中,当直线DA与直线BC垂直时它们的所成角为90°,
此时两条直线所成的角的余弦值为0,达到最小值.
当点A满足直线BC与OA平行时,DA与BC所成的角等于∠OAD,由直线与平面所成角的性质,可得此时两条直线所成的角达到最小值,余弦值达到最大值.
∵DA=DB=DC=1,且DA,DB,DC两两互相垂直,
∴AB=BC=CA![]() ,得到△ABC是边长为
,得到△ABC是边长为![]() 的等边三角形,
的等边三角形,
因此圆O的半径R![]() AB
AB![]() ,
,
设直线BC与OA平行时的点A的位置为A',
∴Rt△AOD中,cos∠OA'D![]() ,即DA与BC所成的余弦值最大值为
,即DA与BC所成的余弦值最大值为![]() ,
,
综上所述,直线DA与直线BC所成角余弦值的取值范围是[0,![]() ].
].