题目内容
 若数列{an},{bn}中,a1=a,b1=b,
若数列{an},{bn}中,a1=a,b1=b,
|
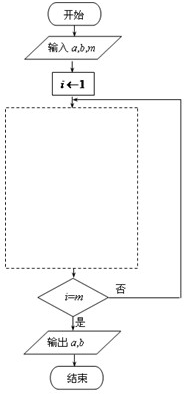
(1)可考虑利用算法来求am,bm的值,其中m为给定的数据(m≥2,m∈N).右图算法中,虚线框中所缺的流程,可以为下面A、B、C、D中的
ACD
ACD
(请填出全部答案)
A、
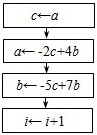 B、
B、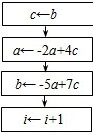
C、
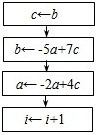 D、
D、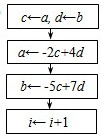
(2)我们可证明当a≠b,5a≠4b时,{an-bn}及{5an-4bn}均为等比数列,请按答纸题要求,完成一个问题证明,并填空.
证明:{an-bn}是等比数列,过程如下:an-bn=(-2an-1+4bn-1)+(5an-1-7bn-1)=3an-1-3bn-1=3(an-1-bn-1)
所以{an-bn}是以a1-b1=a-b≠0为首项,以
3
3
为公比的等比数列;同理{5an-4bn}是以5a1-4b1=5a-4b≠0为首项,以
2
2
为公比的等比数列(3)若将an,bn写成列向量形式,则存在矩阵A,使
|
|
|
|
|
①写出矩阵A=
|
|
P=
,Q=
|
|
P=
,Q=
; ③矩阵Cn中的唯一元素是
|
|
2n+2-4
2n+2-4
.计算过程如下:
分析:(1)根据数列{an},{bn}中的递推关系可知只有B选项不正确,从而得出正确答案;
(2)结合证明过程,根据等比数列的定义知:答案为:3,2;
(3)由于矩阵Bn中所有元素的和等于A,A2,A3,…An中所有元素的和的和,于是可先求An中四个元素之和.
解法一:由
=An-1
⇒
=An
,利用问题(2),得出
从而有:An中元素之和为2×2n,最后Bn中所有元素的和即得;
解法二:由
=An-1
⇒
=An
,可知当a1=b1=1时,An中元素之和就等于an+1+bn+1,于是由问题(2)可知当a=b=1时an-bn=3(an-1-bn-1)=…=0,即an=bn,于是由an=-2an-1+4bn-1=2an-1⇒an=2n-1,即得;
解法三:注意到AQ=
=
=2Q,于是AnQ=An-1(AQ)=A^n-1所以PAnQ=P(2n
)=2n
=2n+1于是Cn=22+23+…2n+1=2n+2-4.
(2)结合证明过程,根据等比数列的定义知:答案为:3,2;
(3)由于矩阵Bn中所有元素的和等于A,A2,A3,…An中所有元素的和的和,于是可先求An中四个元素之和.
解法一:由
|
|
|
|
|
从而有:An中元素之和为2×2n,最后Bn中所有元素的和即得;
解法二:由
|
|
|
|
解法三:注意到AQ=
|
|
|
|
|
|
解答:解:(1)根据数列{an},{bn}中的递推关系可知只有B选项不正确,答案:ACD …(3分)
(2)结合证明过程,根据等比数列的定义知:答案为:
3 2
(3)答案:A=
,一组P,Q的值可以为P=
,Q=
(满足P=
,Q=
形式即可) 矩阵Cn中唯一元素为2n+2-4.
解:由于矩阵Bn中所有元素的和等于A,A2,A3,…An中所有元素的和的和,于是可先求An中四个元素之和.
(填空,可利用能进行矩阵运算的计算器大概两分钟可得出A,A2,A3,A4,计算和分别为4,8,16,32归纳得出An中元素之和为4×2n-1,但An的通项很难归纳得出)
解法一:由
=An-1
⇒
=An
,利用问题(2),得出
⇒
于是
所以An=
,An中元素之和为2×2n,
从而Bn中所有元素的和为22+23+24+…+2n+1=2n+2-4.
解法二:由
=An-1
⇒
=An
,可知当a1=b1=1时,An中元素之和就等于an+1+bn+1,于是由问题(2)可知当a=b=1时an-bn=3(an-1-bn-1)=…=0,即an=bn,于是由an=-2an-1+4bn-1=2an-1⇒an=2n-1,
所以an+1+bn+1=2an+1=2×2n,即An的元素之和为2n+1,从而Bn中所有元素的和为22+23+24+…+2n+1=2n+2-4.
解法三:注意到AQ=
=
=2Q,
于是AnQ=An-1(AQ)=A^n-1
所以PAnQ=P(2n
)=2n
=2n+1
于是Cn=22+23+…2n+1=2n+2-4
(注:解法三不具有通用性,本题中恰好AQ=2Q,于是运算可进行下去.)
故答案为:ACD;2,3;
,P=
(2)结合证明过程,根据等比数列的定义知:答案为:
3 2
(3)答案:A=
|
|
|
|
|
解:由于矩阵Bn中所有元素的和等于A,A2,A3,…An中所有元素的和的和,于是可先求An中四个元素之和.
(填空,可利用能进行矩阵运算的计算器大概两分钟可得出A,A2,A3,A4,计算和分别为4,8,16,32归纳得出An中元素之和为4×2n-1,但An的通项很难归纳得出)
解法一:由
|
|
|
|
|
|
于是
|
所以An=
|
从而Bn中所有元素的和为22+23+24+…+2n+1=2n+2-4.
解法二:由
|
|
|
|
所以an+1+bn+1=2an+1=2×2n,即An的元素之和为2n+1,从而Bn中所有元素的和为22+23+24+…+2n+1=2n+2-4.
解法三:注意到AQ=
|
|
|
于是AnQ=An-1(AQ)=A^n-1
所以PAnQ=P(2n
|
|
|
于是Cn=22+23+…2n+1=2n+2-4
(注:解法三不具有通用性,本题中恰好AQ=2Q,于是运算可进行下去.)
故答案为:ACD;2,3;
|
| 
练习册系列答案
 补充习题江苏系列答案 补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案 学练快车道口算心算速算天天练系列答案
相关题目
|
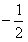 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;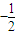 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;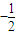 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;