题目内容
对于数列{un}若存在常数M>0,对任意的n∈N+,恒有|un+1-un|+|un-un-1|+…+|u2-u1|≤M则称数列{un}为B-数列。
(1)首项为1,公比为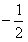 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;
(2)设Sn是数列{xn}的前n项和,给出下列两组判断:
A组:①数列{xn}是B-数列;②数列{xn}不是B-数列
B组:③数列{Sn}是B-数列;④数列{Sn}不是B-数列
请以其中一组的一个论断条件,另一组中的一个论断为结论组成一个命题判断所给命题的真假,并证明你的结论;
(3)若数列{an}是B-数列,证明:数列{an2}也是B-数列。
(1)首项为1,公比为
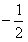 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;(2)设Sn是数列{xn}的前n项和,给出下列两组判断:
A组:①数列{xn}是B-数列;②数列{xn}不是B-数列
B组:③数列{Sn}是B-数列;④数列{Sn}不是B-数列
请以其中一组的一个论断条件,另一组中的一个论断为结论组成一个命题判断所给命题的真假,并证明你的结论;
(3)若数列{an}是B-数列,证明:数列{an2}也是B-数列。
解:(1)设满足题设的等比数列为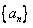
则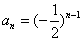
于是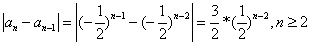
|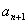 -
-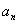 |+|
|+|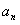 -
-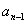 |+…+|
|+…+|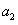 -
-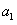 |
|
=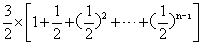
=3×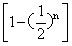 <3
<3
所以首项为1,公比为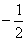 的等比数列是B-数列。
的等比数列是B-数列。
(2)命题1:若数列{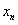 }是B-数列,则数列{Sn}是B-数列
}是B-数列,则数列{Sn}是B-数列
此命题为假命题
事实上设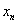 =1,n∈N,
=1,n∈N,
易知数列{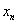 }是B-数列,但Sn=n,
}是B-数列,但Sn=n,
|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|=n
由n的任意性知,数列{Sn}不是B-数列。
命题2:若数列{Sn}是B-数列,则数列{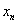 }是B-数列。
}是B-数列。
此命题为真命题。
事实上,因为数列{Sn}是B-数列,
所以存在正数M,对任意的n∈N,
有|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|≤M
即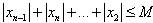
于是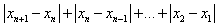
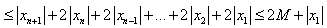
所以数列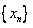 是
是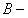 数列。
数列。
(3)数列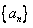 是
是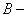 数列,则存在正数M,对任意的
数列,则存在正数M,对任意的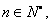 有
有
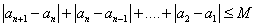
因为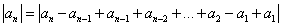
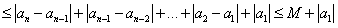
设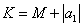 ,则有
,则有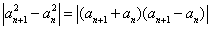
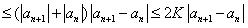
因此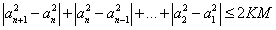
故数列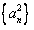 是
是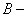 数列。
数列。
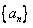
则
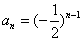
于是
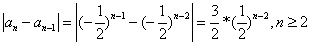
|
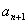 -
-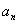 |+|
|+|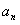 -
-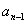 |+…+|
|+…+|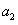 -
-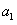 |
|=
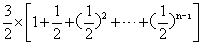
=3×
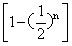 <3
<3所以首项为1,公比为
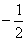 的等比数列是B-数列。
的等比数列是B-数列。(2)命题1:若数列{
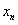 }是B-数列,则数列{Sn}是B-数列
}是B-数列,则数列{Sn}是B-数列此命题为假命题
事实上设
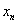 =1,n∈N,
=1,n∈N,易知数列{
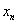 }是B-数列,但Sn=n,
}是B-数列,但Sn=n,|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|=n
由n的任意性知,数列{Sn}不是B-数列。
命题2:若数列{Sn}是B-数列,则数列{
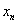 }是B-数列。
}是B-数列。此命题为真命题。
事实上,因为数列{Sn}是B-数列,
所以存在正数M,对任意的n∈N,
有|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|≤M
即
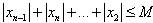
于是
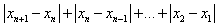
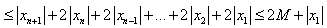
所以数列
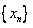 是
是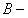 数列。
数列。(3)数列
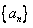 是
是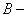 数列,则存在正数M,对任意的
数列,则存在正数M,对任意的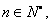 有
有 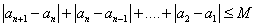
因为
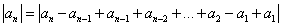
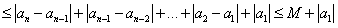
设
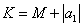 ,则有
,则有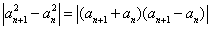
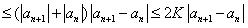
因此
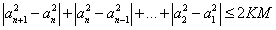
故数列
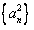 是
是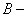 数列。
数列。
练习册系列答案
相关题目
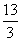 ,
,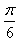 处取得最大值,且最大值为a3,求函数f(x)的解析式.
处取得最大值,且最大值为a3,求函数f(x)的解析式. 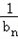 }的前n项和.
}的前n项和.