题目内容
对于数列{un}若存在常数M>0,对任意的n∈N+,恒有|un+1-un|+|un-un1|+…+|u2-u1|≤M则称数列un为B-数列(1)首项为1,公比为-
| 1 | 2 |
(2)设sn是数列{xn}的前n项和,给出下列两组判断:
A组:①数列{xn}是B-数列. ②数列{xn}不是B-数列.
B组 ③数列{sn}是B-数列. ④数列{sn}不是B-数列
请以其中一组的一个论断条件,另一组中的一个论断为结论组成一个命题判断所给命题的真假,并证明你的结论;
(3)若数列{an}是B-数列,证明:数列{an2}也是B-数列.
分析:(1)根据B-数列的定义,首项为1,公比为q=
的等比数列,验证|un+1-un|+|un-un-1|+…+|u2-u1|≤M即可;
(2)首项写出两个命题,根据B-数列的定义加以证明,如果要说明一个命题不正确,则只需举一反例即可;
(3)数列{an}都是B-数列,则有|an+1-an|+|an-an-1|+…+|a2-a1|≤M1下面只需验证|an+12-an2|+|an2-an-12|+…+|a22-a12|≤M.
| 1 |
| 2 |
(2)首项写出两个命题,根据B-数列的定义加以证明,如果要说明一个命题不正确,则只需举一反例即可;
(3)数列{an}都是B-数列,则有|an+1-an|+|an-an-1|+…+|a2-a1|≤M1下面只需验证|an+12-an2|+|an2-an-12|+…+|a22-a12|≤M.
解答:解:(1)设满足题设的等比数列为an,
则an=(-
)n-1.
于是|an-an-1| =|(-
)n-1-(-
)n-2|=
×(
)n-2n≥2
|an+1-an|+|an-an-1|+…+|a2-a1|
=
×[1+
+(
)2+…+(
)n-1]
=3×[1-(
)n] <3,所以首项为1,公比为-
的等比数列是B-数列.
(2)命题1:若数列xn是B-数列,
则数列Sn是B-数列.此命题为假命题.
事实上设xn=1(n∈N*),易知数列xn是B-数列,但Sn=n,
|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|=n.
由n的任意性知,数列Sn不是B-数列.
命题2:若数列Sn是B-数列,
则数列xn不是B-数列.此命题为真命题.
事实上,因为数列Sn是B-数列,
所以存在正数M,对任意的n∈N*,
有|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|≤M,
即|xn+1|+|xn|+…+|x2|≤M.
于是|xn+1-xn|+|xn-xn-1|+…+|x2-x1|≤|xn+1|+2|xn|+2|xn-1|+…+2|x2|+|x1|≤2M+|x1|,
所以数列xn是B-数列.
(3)若数列是{an}B-数列,则存在正数M,对任意的n∈N*有
|an+1-an|+|an-an-1|+…+|a2-a1|≤M
因为|an|=|an-an-1+an-1+an-2+…+a2-a1+a1|≤|an-an-1|+|an-1-an-2|+…+|a2-a1|+|a1|≤M+|a1|
记K=M+|a1|,则有|an+12-an2|=|(an+1+an)(an+1-an)
≤(|an+1|+|an|)|an+1-an|≤2K|an+1-an|
因此|an+12-an2|+|an2-an-12|+…+|a22-a12|≤2KM
故数列{an2}是B-数列.
则an=(-
| 1 |
| 2 |
于是|an-an-1| =|(-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
|an+1-an|+|an-an-1|+…+|a2-a1|
=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=3×[1-(
| 1 |
| 2 |
| 1 |
| 2 |
(2)命题1:若数列xn是B-数列,
则数列Sn是B-数列.此命题为假命题.
事实上设xn=1(n∈N*),易知数列xn是B-数列,但Sn=n,
|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|=n.
由n的任意性知,数列Sn不是B-数列.
命题2:若数列Sn是B-数列,
则数列xn不是B-数列.此命题为真命题.
事实上,因为数列Sn是B-数列,
所以存在正数M,对任意的n∈N*,
有|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|≤M,
即|xn+1|+|xn|+…+|x2|≤M.
于是|xn+1-xn|+|xn-xn-1|+…+|x2-x1|≤|xn+1|+2|xn|+2|xn-1|+…+2|x2|+|x1|≤2M+|x1|,
所以数列xn是B-数列.
(3)若数列是{an}B-数列,则存在正数M,对任意的n∈N*有
|an+1-an|+|an-an-1|+…+|a2-a1|≤M
因为|an|=|an-an-1+an-1+an-2+…+a2-a1+a1|≤|an-an-1|+|an-1-an-2|+…+|a2-a1|+|a1|≤M+|a1|
记K=M+|a1|,则有|an+12-an2|=|(an+1+an)(an+1-an)
≤(|an+1|+|an|)|an+1-an|≤2K|an+1-an|
因此|an+12-an2|+|an2-an-12|+…+|a22-a12|≤2KM
故数列{an2}是B-数列.
点评:考查学生理解数列概念,灵活运用数列表示法的能力,旨在考查学生的观察分析和归纳能力,特别是问题(2)(3)的设置,增加了题目的难度,同时也考查了等差数列的定义和分类讨论的思想,属难题.

练习册系列答案
相关题目
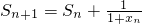 ,
,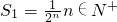
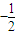 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;