题目内容
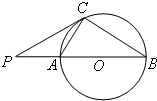 (2013•门头沟区一模)如图:圆O的割线PAB经过圆心O,C是圆上一点,PA=AC=
(2013•门头沟区一模)如图:圆O的割线PAB经过圆心O,C是圆上一点,PA=AC=| 1 |
| 2 |
分析:根据AB是圆的直径结合AC=
AB,得到△ACB中∠B=30°,∠CAB=60°且BC=
AB.再在△PAC中用余弦定理,计算出PC=
AC=
AB,从而得到BC=PC,可得A、B两项都正确;连接OC,算出∠PCO=90°,可得PC⊥CO,从而PC是圆O的切线,C正确;最后根据切割线定理,结合前面算出的数据得到BC2≠BA•BP,得D不正确.
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
解答:解:∵AB是圆O的直径,∴∠ACB=90°
又∵AC=
AB,∴∠B=30°,可得∠CAB=60°且BC=
AB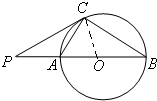
∵PA=AC=
AB,
∴△PAC用余弦定理,
得PC=
=
AC=
AB,
即BC=PC,得A正确;
∵PA=AC,BC=PC,∴PC•AC=PA•BC,得B正确;
连接OC,可得
∵等腰△PAC中,∠PCA=30°且等边△ACO中,∠ACO=60°
∴∠OCP=90°,可得PC⊥OC,所以PC是圆O的切线,故C正确;
根据切割线定理,得BC2=PC2=PA•PB≠BA•BP,故D不正确.
故选:D
又∵AC=
| 1 |
| 2 |
| ||
| 2 |

∵PA=AC=
| 1 |
| 2 |
∴△PAC用余弦定理,
得PC=
| PA2+AC2-2PA•ACcos120° |
| 3 |
| ||
| 2 |
即BC=PC,得A正确;
∵PA=AC,BC=PC,∴PC•AC=PA•BC,得B正确;
连接OC,可得
∵等腰△PAC中,∠PCA=30°且等边△ACO中,∠ACO=60°
∴∠OCP=90°,可得PC⊥OC,所以PC是圆O的切线,故C正确;
根据切割线定理,得BC2=PC2=PA•PB≠BA•BP,故D不正确.
故选:D
点评:本题给出圆的切线与经过圆心的割线,判断几个命题的真假,着重考查了圆的切线的判定定理、含有30度角直角三角形的性质、切割线定理和余弦定理等知识,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 (2013•门头沟区一模)如图已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.
(2013•门头沟区一模)如图已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.