题目内容

2．若函数f（x）=$\left\{\begin{array}{l}{（x-1）^{2}，x∈[0，+∞）}\\{x+1，x∈（-∞，0）}\end{array}\right.$，则f（x）的单调增区间是（-∞，0]，[1，+∞）．

分析 画出分段函数f（x）=$\left\{\begin{array}{l}{（x-1）^{2}，x∈[0，+∞）}\\{x+1，x∈（-∞，0）}\end{array}\right.$的图象，数形结合可得f（x）的单调增区间．

解答 解：∵函数f（x）=$\left\{\begin{array}{l}{（x-1）^{2}，x∈[0，+∞）}\\{x+1，x∈（-∞，0）}\end{array}\right.$的图象如下图所示：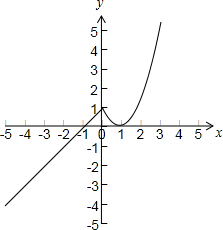

由图可得：f（x）的单调增区间是：（-∞，0]，[1，+∞），
故答案为：（-∞，0]，[1，+∞）

点评 本题考查的知识点是分段函数的应用，熟练掌握并正确理解分段函数的单调性，是解答的关键．

练习册系列答案
相关题目
12．函数y=f（x）的图象上不同两点A（x1，y1），B（x2，y2）处的切线的斜率分别是kA，kB，规定φ（A，B）=$\frac{|{k}_{A}-{k}_{B}|}{|AB|}$叫做曲线y=f（x）在点A与点B之间的“弯曲度”．设曲线y=ex上不同两点A（x1，y1），B（x2，y2），且x1-x2=1，若t•φ（A，B）＜1恒成立，试求实数t的取值范围．
13．比较下列各组数的大小．
（1）1.5${\;}^{\frac{1}{3}}$，1.7${\;}^{\frac{1}{3}}$，1；
（2）（-$\frac{\sqrt{2}}{2}$）${\;}^{-\frac{2}{3}}$，（-$\frac{10}{7}$）${\;}^{\frac{2}{3}}$，1.1${\;}^{-\frac{4}{3}}$；
（3）3.8${\;}^{-\frac{2}{3}}$，3.9${\;}^{\frac{2}{5}}$，（-1.8）${\;}^{\frac{3}{5}}$；
（4）31.4，51.5．
10．证明整数指数幂的运算性质am•an=am+n．
17．1g2+1g100${\;}^{\frac{1}{2}-lg\sqrt{2}}$的值为（　　）
A．1B．2C．-1D．-2
7．化简：
（1）$\frac{{a}^{\frac{4}{3}}-8{a}^{\frac{1}{3}}b}{4{b}^{\frac{2}{3}}+2{a}^{\frac{1}{3}}{b}^{\frac{1}{3}}+{a}^{\frac{2}{3}}}$÷（1-2$\frac{\root{3}{b}}{\root{3}{a}}$）×$\root{3}{a}$；
（2）$\frac{x-y}{{x}^{\frac{1}{3}}-{y}^{\frac{1}{3}}}$-$\frac{x+y}{{x}^{\frac{1}{3}}+{y}^{\frac{1}{3}}}$．
14．已知抛物线y=x2+4x+7，求将这条抛物线平移到顶点与坐标原点重合时的函数解析式．
11．下面各选项中，两个集合相等的是（　　）
A．M={（1，2）}，N={（2，1）}B．M=（1，2），N={（1，2）}
C．M=∅，N={0}D．M={x|x2-3x+2=0}，N={1，2}
12．如图，正方形ABCD与矩形ACEF所在平面互相垂直，AB=$\sqrt{2}$，AF=1，M在EF上，且AM∥平面BDE，则M点的坐标为（　　）
A．（1，1，1）B．（$\frac{\sqrt{2}}{3}$，$\frac{\sqrt{2}}{3}$，1）C．（$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{2}}{2}$，1）D．（$\frac{\sqrt{2}}{4}$，$\frac{\sqrt{2}}{4}$，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网