Question

【题目】已知函数f（x）=lg ，f（1）=0，且f（2）﹣f（ ）=lg2．
（1）求f（x）的表达式；
（2）若x∈（0，+∞）时方程f（x）=lgt有解，求实数t的取值范围；
（3）若函数y=f（x）﹣lg（8x+m）的无零点，求实数m的取值范围．

Answer 1

【答案】
（1）解：∵且f（2）﹣f（ ）=lg2，即x＞0时，f（x）﹣f（ ）=lgx．

lg ﹣lg =lgx，

即lg﹣lg=lgx，

即lg（ ）=lgx， =x．

整理得（a﹣b）x2﹣（a﹣b）x=0恒成立，

∴a=b，

又f（1）=0，

即a+b=2，从而a=b=1．

∴f（x）=lg ，

∵ ＞0，

∴x＜﹣1，或x＞0，

∴f（x）的定义域为（﹣∞，﹣1）∪（0，+∞）

（2）解：方程f（x）=lgt有解，

即lg =lgt，

∴t= ，

∴x（2﹣t）=t，

∴x= ，

∴ ＜﹣1，或 ＞0，

解得t＞2，或0＜t＜2，

∴实数t的取值范围（0，2）∪（2，+∞）

（3）解：函数y=f（x）﹣lg（8x+m）的无零点即方程f（x）=lg（8x+m）的解集为，

∴lg =lg（8x+m），

∴ =8x+m，

∴8x2+（6+m）x+m=0，

方程的解集为，故有两种情况：

①方程8x2+（6+m）x+m=0无解，即△＜0，得2＜m＜18，

②方程8x2+（6+m）x+m=0有解，两根均在[﹣1，0]内，g（x）=8x2+（6+m）x+m，

则 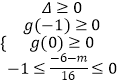，解得：0≤m≤2，

综合①②得实数m的取值范围是0≤m＜18

【解析】（1）由已知中函数，以构造一个关于a，b方程组，解方程组求出a，b值，进而得到f（x）的表达式；（2）由（1）中函数f（x）的表达式，转化为一个方程，分离参数，根据f（x）的定义域即可求出；（3）根据对数的运算性质，可将方程f（x）=lg（8x+m），转化为一个关于x的分式方程组，进而根据方程f（x）=lg（8x+m）的解集为，则方程组至少一个方程无解，或两个方程的解集的交集为空集，分类讨论后，即可得到答案．