题目内容
14.已知函数g(x)=x2-3;f(x)是定义在 (-∞,0)∪(0,+∞)上的奇函数,且当x>0时,f(x)=log2x;那么函数y=f(x)•g(x)的大致图象为( )| A. | 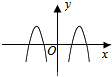 | B. |  | C. | 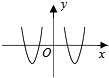 | D. | 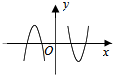 |
分析 函数y=f(x)•g(x)为奇函数,它的图象关于原点对称,故排除A、C.再根据函数y=f(x)•g(x)在(3,+∞)上单调递增,故排除B,从而得出结论.
解答 解:由于函数g(x)=x2-3为偶函数,f(x)为奇函数,故函数y=f(x)•g(x)为奇函数,
它的图象关于原点对称,故排除A、C.
再根据当x>0时,f(x)=log2x,
可得当x>0时,函数y=f(x)•g(x)=(x2-3)(log2x)在(3,+∞)上单调递增,故排除B,
故选:D.
点评 本题主要考查函数的图象特征,函数的奇偶性、单调性的应用,属于中档题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
4.在△ABC中,角A、B、C的对边分别为a、b、c,已知A=$\frac{π}{6}$,a=1,b=2,则c=( )
| A. | $1或\sqrt{3}$ | B. | $2或\sqrt{3}$ | C. | $\sqrt{3}-1$ | D. | $\sqrt{3}$ |
6.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为$\frac{3}{5}$.
(1)请将上面的列联表补充完整;
(2)是否有99%以上的把握认为喜爱打篮球与性别有关?说明你的理由.
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
(1)请将上面的列联表补充完整;
(2)是否有99%以上的把握认为喜爱打篮球与性别有关?说明你的理由.
3.用反证法证明命题:“若(a-1)(b-1)(c-1)>0,则a,b,c中至少有一个大于1”时,下列假设中正确的是( )
| A. | 假设a,b,c都大于1 | B. | 假设a,b,c中至多有一个大于1 | ||
| C. | 假设a,b,c都不大于1 | D. | 假设a,b,c中至多有两个大于1 |