题目内容
【题目】如图1所示,在等腰梯形![]() ,
,![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() .将
.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,如图2所示,点
,如图2所示,点![]() 为棱
为棱![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)在图1的等腰梯形![]() 内,过
内,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,可得四边形
,可得四边形![]() 为正方形,且
为正方形,且![]() ,
,![]() 为
为![]() 中点.在图2中,连结
中点.在图2中,连结![]() ,证明
,证明![]() .结合
.结合![]() ,利用平面与平面平行的判定可得平面
,利用平面与平面平行的判定可得平面![]() 平面
平面![]() ,从而得到
,从而得到![]() 平面
平面![]() ;
;
(2)由平面![]() 平面
平面![]() ,
,![]() ,得
,得![]() 平面
平面![]() .进一步得到
.进一步得到![]() .求解三角形证明
.求解三角形证明![]() .再由线面垂直的判定可得
.再由线面垂直的判定可得![]() 平面
平面![]() ;
;
(3)证明![]() 面
面![]() ,可得线段
,可得线段![]() 为三棱锥
为三棱锥![]() 底面
底面![]() 的高,然后利用等积法求三棱锥
的高,然后利用等积法求三棱锥![]() 的体积.
的体积.
(1)在如图的等腰梯形![]() 内,
内,
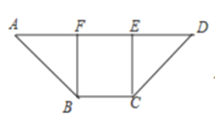
过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
∵![]() ,
,
∴ ![]() ,
,
又∵![]() ,
,![]() ,
,![]() ,
,
∴ 四边形![]() 为正方形,且
为正方形,且![]() ,
,![]() 为
为![]() 中点.
中点.
在如图中,
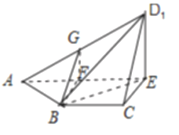
连结![]() ,
,
∵ 点![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
又∵ ![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
∴ 平面![]() 平面
平面![]() ,
,
又∵ ![]() 面
面![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)∵ 平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
∴ ![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,
,
∴![]() .
.
又![]() ,
,![]() ,
,![]() ,满足
,满足![]() ,
,
∴![]() .
.
又![]() ,
,
![]() 平面
平面![]() ;
;
(3)∵![]() ,
,![]() ,
,![]() ,
,
∴ ![]() 面
面![]() .
.
又线段![]() 为三棱锥
为三棱锥![]() 底面
底面![]() 的高,
的高,
∴ ![]() .
.

【题目】平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第![]() 条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以
条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以![]() 元罚款,记
元罚款,记![]() 分的行政处罚.如表是本市一主干路段监控设备所抓拍的
分的行政处罚.如表是本市一主干路段监控设备所抓拍的![]() 个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
违章驾驶员人数 |
|
|
|
|
|
(Ⅰ)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(Ⅱ)预测该路段![]() 月份的不“礼让斑马线”违章驾驶员人数.
月份的不“礼让斑马线”违章驾驶员人数.
参考公式: ,
,![]() .
.
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了![]() 名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为选手成绩“优秀”与文化程度有关?
的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
(2)若参赛选手共![]() 万人,用频率估计概率,试估计其中优秀等级的选手人数;
万人,用频率估计概率,试估计其中优秀等级的选手人数;
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)求![]()
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据1求出的线性同归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(附: ![]() ,
,![]() ,
, ,
,![]() ,其中
,其中![]() ,
,![]() 为样本平均值)
为样本平均值)