题目内容
已知数列 的前
的前 项和为
项和为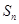 ,数列
,数列 是公比为
是公比为 的等比数列,
的等比数列, 是
是 和
和 的等比中项.
的等比中项.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
(1)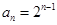 ;(2)
;(2) .
.
解析试题分析:(1)数列中可根据通项 的特点选择对应的方法来求
的特点选择对应的方法来求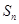 ,反之也可根据
,反之也可根据 ,利用
,利用 来再求
来再求 ,此题可先根据条件求出
,此题可先根据条件求出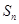 ,然后就不难求
,然后就不难求 了;(2)由(1)不难得到数列
了;(2)由(1)不难得到数列 通项公式,根据通项公式的特点应选择用错位相减法来求数列前
通项公式,根据通项公式的特点应选择用错位相减法来求数列前 项和
项和 .特殊数列的求和方法通常有:①公式法;②分解法;③拆项相消法;④错位相减法;⑤奇偶分析法;⑥倒序相加法等等,关键是掌握根据通项所具有的特点来选择对应的求和方法,这份试卷中已经考查了两种特殊数列求和方法——拆项相消法和错位相减法,通常一个等差数列和一个等比数列对应项相乘得到的数列求前
.特殊数列的求和方法通常有:①公式法;②分解法;③拆项相消法;④错位相减法;⑤奇偶分析法;⑥倒序相加法等等,关键是掌握根据通项所具有的特点来选择对应的求和方法,这份试卷中已经考查了两种特殊数列求和方法——拆项相消法和错位相减法,通常一个等差数列和一个等比数列对应项相乘得到的数列求前 项的和时常用错位相减法,这个方法不难掌握,但要把题目做正确还是有一定难度的,故有“人人会做,人人都有可能做不对”一说,所以要特别关注易错之处.
项的和时常用错位相减法,这个方法不难掌握,但要把题目做正确还是有一定难度的,故有“人人会做,人人都有可能做不对”一说,所以要特别关注易错之处.
试题解析:(1)∵ 是公比为
是公比为 的等比数列,∴
的等比数列,∴ ,
,
∴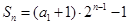 ,从而
,从而 ,
,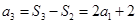 ,
,
∵ 是
是 和
和 的等比中项,∴
的等比中项,∴ ,解得
,解得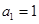 或
或 ,
,
当 时,
时, ,
, 不是等比数列,∴
不是等比数列,∴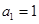 ,∴
,∴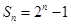 ,
,
当 时,
时,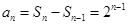 ,∵
,∵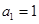 符合
符合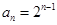 ,∴
,∴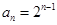 ; (6分)
; (6分)
(2)∵ ,
,
∴ ①
①
① 得:
得: ②
②
① ②得:
②得:
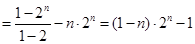 ,
,
∴ . (14分)
. (14分)
考点:1.等比数列通项公式及前 项和公式;2.等比中项;3.特殊数列求和方法之一:错位相减法.
项和公式;2.等比中项;3.特殊数列求和方法之一:错位相减法.

练习册系列答案
相关题目
 的公比
的公比 大于1,若向量
大于1,若向量
 ,
, ,满足
,满足 ,则
,则 _____________
_____________ 所有项均为正数,首
所有项均为正数,首 ,且
,且 成等差数列.
成等差数列. 的前n项和为
的前n项和为 ,若
,若 ,求实数
,求实数 的值.
的值.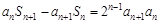 ,
,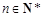 .
.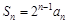 ;
; ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn. ,
,  满足条件:
满足条件:
 ,
,  .
. 是等比数列,并求数列
是等比数列,并求数列 项和
项和 ,并求使得
,并求使得 对任意
对任意 N*都成立的正整数
N*都成立的正整数 的最小值.
的最小值. 的前
的前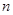 项和为
项和为 ,且
,且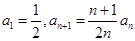 .
.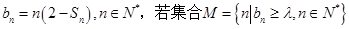 恰有5个元素,求实数
恰有5个元素,求实数 的取值范围.
的取值范围. 的前
的前 项和为
项和为 ,数列
,数列 是公比为
是公比为 的等比数列,
的等比数列, 是
是 和
和 的等比中项.
的等比中项. 的前
的前 .
. 中, 若
中, 若 是方程
是方程 的两根,则
的两根,则 = .
= .