题目内容
14.已知函数f(x)=lnx-bx+c,f(x)在点(1,f(1))处的切线方程为x+y+4=0(Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)若在区间[$\frac{1}{2}$,5]内,恒有f(x)≥x2+lnx+kx成立,求k的取值范围.
分析 (Ⅰ)由求导公式、法则求出f′(x),根据题意和导数的几何意义求出b的值,将(1,f(1))代入方程x+y+4=0求出f(1),代入解析式列出方程求出c,即可求出函数f(x)的解析式;
(Ⅱ)由(I)求出函数的定义域和f′(x),求出f′(x)>0和f′(x)<0的解集,即可求出函数f(x)的单调区间;
(Ⅲ)先化简f(x)≥x2+lnx+kx,并分离常数k,再构造函数g(x)=$-x-2-\frac{3}{x}$,求出g′(x)并求出g′(x)大于、小于零的解集,求出g(x)的单调区间和最小值,再求出k的取值范围.
解答 解:(Ⅰ)由题意得,f′(x)=$\frac{1}{x}-b$,则f′(1)=1-b,
∵在点(1,f(1))处的切线方程为x+y+4=0,
∴切线斜率为-1,则1-b=-1,得b=2 …2分
将(1,f(1))代入方程x+y+4=0得:1+f(1)+4=0,解得f(1)=-5,
∴f(1)=-b+c=-5,将b=2代入得c=-3,
故f(x)=lnx-2x-3 …5分
(Ⅱ)依题意知函数的定义域是(0,+∞),且$f′(x)=\frac{1}{x}-2$,
令f′(x)>0得,$0<x<\frac{1}{2}$,令f′(x)<0得,$x>\frac{1}{2}$,
故f(x)的单调增区间为(0,$\frac{1}{2}$),单调减区间为($\frac{1}{2}$,+∞) …9分
(Ⅲ)由f(x)≥x2+lnx+kx得,lnx-2x-3≥x2+lnx+kx,
∴k≤$-x-2-\frac{3}{x}$在区间[$\frac{1}{2}$,5]内恒成立,…10分
设g(x)=$-x-2-\frac{3}{x}$,则g′(x)=$-1+\frac{3}{{x}^{2}}$,
令g′(x)=0得,x=$\sqrt{3}$或x=$-\sqrt{3}$(负值舍去),
令g′(x)>0得$0<x<\sqrt{3}$,令g′(x)<0得$x>\sqrt{3}$,
故在($\frac{1}{2}$,$\sqrt{3}$)上g(x)单调递增,在($\sqrt{3}$,5)上g(x)单调递减,
∴g(x)的最小值只能在区间[$\frac{1}{2}$,5]的端点处取得 …12分
∵g($\frac{1}{2}$)=$-\frac{1}{2}-2-6$=$-\frac{17}{2}$,g(5)=-5-2-$\frac{3}{5}$=$-\frac{28}{5}$,
∴g(x)的最小值是g($\frac{1}{2}$)=$-\frac{17}{2}$.
所以k≤$-\frac{17}{2}$,即k的取值范围为(-∞,$-\frac{17}{2}$). …14分.
点评 本题考查求导公式和法则,导数的几何意义,利用导数研究函数的单调性、最值问题,考查分离常数法,转化思想,属于中档题.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案| A. | y=2x | B. | y=2lgx | C. | y=2x3 | D. | y=x+$\frac{2}{x}$ |
| A. | $-\frac{7}{8}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{7}{8}$ |
| A. | $\frac{1}{3}$n(n+1)(n+2) | B. | $\frac{1}{3}$n(n+1)(n+3) | C. | $\frac{1}{3}$n(n+1)(n+4) | D. | $\frac{1}{3}$n(n+1)(n+5) |
(1)请根据上述数据填写2×2列联表:
| 懒惰 | 不懒惰 | 总计 | |
| 女 | |||
| 男 | |||
| 总计 |
临界值表
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
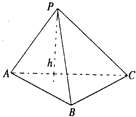 在Rt△ABC中,两直角边分别为a,b,设h为斜边上的高,则$\frac{1}{h^2}$=$\frac{1}{a^2}$+$\frac{1}{b^2}$,类比此性质,如图,在四面体P-ABC 中,若PA,PB,PC两两垂直,且长度分别为a,b,c,设棱锥底面ABC上的高为h,则得到的正确结论为$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$.
在Rt△ABC中,两直角边分别为a,b,设h为斜边上的高,则$\frac{1}{h^2}$=$\frac{1}{a^2}$+$\frac{1}{b^2}$,类比此性质,如图,在四面体P-ABC 中,若PA,PB,PC两两垂直,且长度分别为a,b,c,设棱锥底面ABC上的高为h,则得到的正确结论为$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$. 某同学做了一个如图所示的等腰直角三角形形状的数表,且把奇数和偶数分别依次排在了数表的奇数行和偶数行.若用a(i,j)表示第i行从左数第j个数,如a(4,3)=10,则a(21,6)=211.
某同学做了一个如图所示的等腰直角三角形形状的数表,且把奇数和偶数分别依次排在了数表的奇数行和偶数行.若用a(i,j)表示第i行从左数第j个数,如a(4,3)=10,则a(21,6)=211.