题目内容
已知函数f(x)=cos(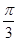 +x)·cos(
+x)·cos(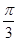 -x),g(x)=
-x),g(x)=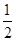 sin2x-
sin2x-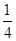 .
.
(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
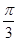 +x)·cos(
+x)·cos(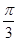 -x),g(x)=
-x),g(x)=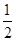 sin2x-
sin2x-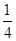 .
.(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
(1)π
(2){x|x=kπ-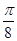 ,k∈Z}
,k∈Z}
(2){x|x=kπ-
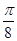 ,k∈Z}
,k∈Z}解:(1)因为f(x)=cos(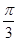 +x)cos(
+x)cos(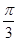 -x)
-x)
=(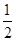 cosx-
cosx-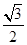 sinx)(
sinx)(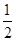 cosx+
cosx+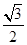 sinx)
sinx)
=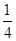 cos2x-
cos2x-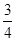 sin2x
sin2x
=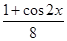 -
-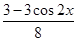
=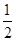 cos2x-
cos2x-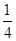 ,
,
所以f(x)的最小正周期为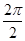 =π.
=π.
(2)h(x)=f(x)-g(x)=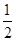 cos2x-
cos2x-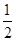 sin2x
sin2x
=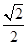 cos(2x+
cos(2x+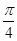 ),
),
当2x+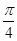 =2kπ(k∈Z)时,h(x)取得最大值
=2kπ(k∈Z)时,h(x)取得最大值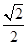 .
.
所以h(x)取得最大值时,对应的x的集合为{x|x=kπ-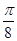 ,k∈Z}.
,k∈Z}.
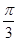 +x)cos(
+x)cos(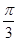 -x)
-x)=(
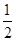 cosx-
cosx-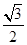 sinx)(
sinx)(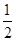 cosx+
cosx+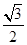 sinx)
sinx)=
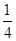 cos2x-
cos2x-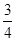 sin2x
sin2x=
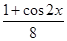 -
-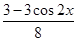
=
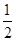 cos2x-
cos2x-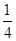 ,
,所以f(x)的最小正周期为
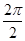 =π.
=π.(2)h(x)=f(x)-g(x)=
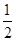 cos2x-
cos2x-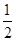 sin2x
sin2x=
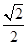 cos(2x+
cos(2x+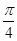 ),
),当2x+
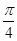 =2kπ(k∈Z)时,h(x)取得最大值
=2kπ(k∈Z)时,h(x)取得最大值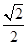 .
.所以h(x)取得最大值时,对应的x的集合为{x|x=kπ-
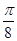 ,k∈Z}.
,k∈Z}.
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 ,
,
 ;
; 。
。 是( )
是( ) 的偶函数
的偶函数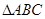 中,内角
中,内角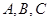 所对的边分别为
所对的边分别为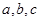 ,且
,且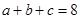
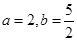 ,求
,求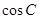 的值;
的值;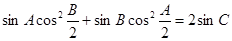 ,且
,且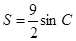 ,求
,求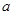 和
和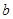 的值.
的值.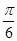 )+sinα=
)+sinα=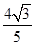 ,则sin(α+
,则sin(α+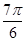 )的值是( )
)的值是( )


 ),满足tan(α+β)=4tanβ,则tanα的最大值是( )
),满足tan(α+β)=4tanβ,则tanα的最大值是( )



 ,
, ,则
,则 ( )
( ) 在区间
在区间 上的最大值为2,则常数a的值为 .
上的最大值为2,则常数a的值为 . ,则
,则 =
=