题目内容
已知命题p：对任意x∈R，总有2x＞0；q：“x＞1”是“x＞2”的充分不必要条件，则下列命题为真命题的是（ ）
| A、p∧q | B、￢p∧￢q | C、￢p∧q | D、p∧￢q |
考点：复合命题的真假,必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：判定命题p，q的真假，利用复合命题的真假关系即可得到结论．
解答：解：根据指数函数的性质可知，对任意x∈R，总有2x＞0成立，即p为真命题，
：“x＞1”是“x＞2”的必要不充分条件，即q为假命题，
则p∧￢q，为真命题，
故选：D．
：“x＞1”是“x＞2”的必要不充分条件，即q为假命题，
则p∧￢q，为真命题，
故选：D．
点评：本题主要考查复合命题的真假关系的应用，先判定p，q的真假是解决本题的关键，比较基础．
练习册系列答案
相关题目
函数y=
在区间[-π，π]上的图象是（ ）
| xcosx |
| x2+1 |
A、 |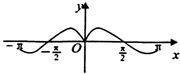
B、 |
C、 |
D、 |
若等差数列{an}的前n项和为Sn，且S3=12，a1=2，则a4=（ ）
| A、20 | B、10 | C、6 | D、8 |
不等式x2+3x+2≥0的解集是（ ）
| A、{x|1≤x≤2} | B、{x|x≤1或x≥2} | C、{x|-2≤x≤-1} | D、{x|x≤-2或x≥-1} |
不等式
≤2的解集是（ ）
| x-2 |
| x+3 |
| A、{x|x＜-8或x＞-3} |
| B、{x|x≤-8或x＞-3} |
| C、{x|-3≤x≤2} |
| D、{x|-3＜x≤2} |
已知命题p，q，则“p∧（?q）为真”是“（?p）∨q为假”的（ ）
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |
如图，点P从点O出发，分别按逆时针方向沿周长均为12的正三角形、正方形运动一周，O，P两点连线的距离y与点P走过的路程x的函数关系分别记为y=f（x），y=g（x），定义函数h（x）=下列四个函数①f（x）=x+1，②f（x）=2x3，③f（x）=xsinx，④f（x）=
的图象能等分圆O：x2+y2=1的面积的是（ ）
| x |
| cosx |
| A、②③ | B、②④ |
| C、②③④ | D、①②③④ |
如图抛物线方程为y2=8x，圆x2+y2-4x=0的圆心为F，过点F斜率为2的直线与抛物线和圆相交于A、B、C、D四点，则|AD|•|BC|的值是（ ）