Question

9、已知函数y=f（x）（x∈R）满足f（x+1）=f（x-1），且x∈[-1，1]时，f（x）=|x|，则函数y=f（x）与y=log₅x的图象的交点的个数为（　　）

A、1

B、2

C、3

D、4

Answer 1

分析：由条件（x+1）=f（x-1）知函数周期为2，知道f（x）在[-1，1]这一个周期的图象，利用周期可以画出整个定义域上的图象，同时把y=log₅^x的图象画在同一坐标系内，很容易获得答案．

解答：解：因为函数满足f（x+1）=f（x-1），所以其周期为2．在x∈[-1，1]这一个周期上为y=|x|，y=f（x）和y=log₅^x在同一个坐标系的图象如下：

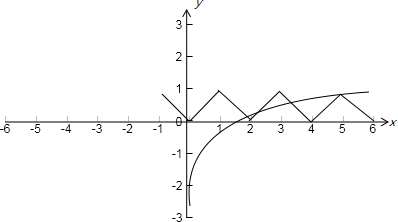
从图象上易知交点个数为4．
故选D

点评：考查函数的周期性，以及数形结合解决问题的能力，注意x=5时的函数值，考查作图能力，计算能力．