题目内容
【题目】在直角坐标系
中，已知中心在原点，离心率为
的椭圆
的一个焦点为圆
： 
的圆心．
（Ⅰ）求椭圆
的方程；
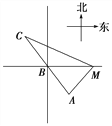
（Ⅱ）设
是椭圆
上一点，过
作两条斜率之积为
的直线
， 
，当直线
， 
都与圆
相切时，求
的坐标．
【答案】（Ⅰ）
（Ⅱ）
，或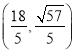
，或
，或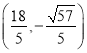
.
【解析】试题分析：（1）圆心坐标是已知的，故椭圆的焦点是已知的，从而半焦距
已知了，又有离心率，故半长轴长
也能求出，从而求出
，而根据题意，椭圆方程是标准方程，可其方程易得；（2）设P点坐标为
，再设一条切线的斜率为
，则另一条切线的斜率为
，三个未知数
需要三个方程，点P在椭圆上，一个等式，两条直线都圆的切线，利用圆心到切线的距离等于圆的半径又得到两个等式，三个等量关系，三个未知数理论上可解了，当然具体解题时，可设切线斜率为
，则点斜率式写出直线方程，利用圆心到切线距离等于圆半径得出关于
的方程，而
是这个方程的两解，由韦达定理得
，这个结果又是
，就列出了关于P点坐标的一个方程，再由P点在椭圆上，可解出P点坐标．
试题解析：（1）圆的标准方程为
，圆心为
，所以
，又
， 
， 
，而据题意椭圆的方程是标准方程，故其方程为
．4分
（2）设
，得
∵
，依题意
到
的距离为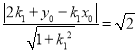
整理得
同理
∴
是方程
的两实根10分
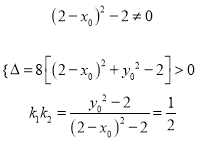12分
∴
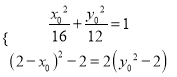14分
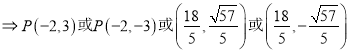16分
练习册系列答案
阅读快车系列答案
相关题目
【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加书法社团 | 2 | 30 |
（1）从该班随机选 1 名同学，求该同学至少参加上述一个社团的概率；
（2）在既参加书法社团又参加演讲社团的 8 名同学中，有 5 名男同学
,3名女同学
.现从这 5 名男同学和 3 名女同学中各随机选 1 人，求
被选中且
未被选中的概率.
