题目内容
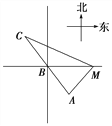
【题目】如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于1 km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,求塔到直路ABC的最短距离.
【答案】![]()
【解析】试题分析:由S△MAB与S△MBC底相同高相同得S△MAB=S△MBC;利用三角形面积公式代入整理得MC=![]() MA,然后根据余弦定理得AC2=MA2+MC2-2MA·MC·cos 75°=
MA,然后根据余弦定理得AC2=MA2+MC2-2MA·MC·cos 75°=![]() MA;最后根据三角形的面积公式得
MA;最后根据三角形的面积公式得![]() MA·MC·sin 75°=
MA·MC·sin 75°=![]() AC·h,整理求出h=
AC·h,整理求出h=![]() (km).
(km).
试题解析:
由题意∠CMB=30°,∠AMB=45°,
因为AB=BC=1,所以S△MAB=S△MBC,
即![]() MA·MB·sin 45°=
MA·MB·sin 45°=![]() MC·MB·sin 30°,
MC·MB·sin 30°,
所以MC=![]() MA,
MA,
在△MAC中,由余弦定理AC2=MA2+MC2-2MA·MC·cos 75°,
所以MA2=![]() ,
,
设M到AB的距离为h,则由△MAC的面积得
![]() MA·MC·sin 75°=
MA·MC·sin 75°=![]() AC·h,
AC·h,
所以h=![]() ·sin 75°=
·sin 75°=![]() ·
·![]() ·sin 75°=
·sin 75°=![]() (km).
(km).

【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满足100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组 | 频数 | 频率 |
| 5 | 0.05 |
|
| 0.20 |
| 35 |
|
| 25 | 0.25 |
| 15 | 0.15 |
合计 | 100 | 1.00 |
(1)求![]() 的值并估计这100名考生成绩的平均分;
的值并估计这100名考生成绩的平均分;
(2)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
【题目】某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如表所示:
资源 消耗量 产品 | 甲产品(每吨) | 乙产品(每吨) | 资源限额(每天) |
煤( | 9 | 4 | 360 |
电力( | 4 | 5 | 200 |
劳力(个) | 3 | 10 | 300 |
利润(万元) | 7 | 12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?