题目内容
18.定义:若两椭圆C1:$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1,{C_2}:\frac{x^2}{{{a_2}^2}}+\frac{y^2}{{{b_2}^2}}$=1满足$\frac{a_2}{a_1}=\frac{b_2}{b_1}$=λ,则称椭圆C1与椭圆C2相似,相似比为λ,现有一系列相似椭圆Cn:$\frac{x^2}{{{a_n}^2}}+\frac{y^2}{{{b_n}^2}}$=1,满足a1=$\sqrt{2}$,b1=1,相似比λ=2,直线l:y=x与这一系列相似椭圆在第一象限内的交点分别为A1,A2,…,An,设αn=|AnAn+1|.(1)求α1;
(2)求证:{an}为等比数列,并求出其通项公式;
(3)令${β_n}={log_2}(\sqrt{3}{α_n})$,求证$\frac{β_1}{β_2}+\frac{{{β_1}•{β_3}}}{{{β_2}•{β_4}}}+…+\frac{{{β_1}•{β_3}•{β_5}…{β_{2n-1}}}}{{{β_2}•{β_4}•{β_6}…{β_{2n}}}}<\sqrt{2{β_n}+1}$-1.
分析 (1)将直线l:y=x与椭圆C1:$\frac{{x}^{2}}{2}+{y}^{2}=1$和椭圆C2:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$联立可得:x1,x2,代入α1=|A1A2|可得答案;
(2)将直线l:y=x与椭圆Cn:$\frac{{x}^{2}}{{2}^{2n-1}}+\frac{{y}^{2}}{{2}^{2n-2}}=1$联立得:xn,代入αn=|AnAn+1|可得结论;
(3)${β_n}={log_2}(\sqrt{3}{α_n})$=$lo{g}_{2}(\sqrt{3}•\frac{\sqrt{3}•{2}^{n}}{3})$=n,利用放缩法可得:$\frac{1}{2}$+$\frac{1•3}{2•4}$+…+$\frac{1×3×5×…×(2n-1)}{2×4×6×…×2n}$<$\sum _{k=1}^{n}\frac{1}{\sqrt{2k+1}}$<$\sqrt{2n+1}-1$,即$\frac{β_1}{β_2}+\frac{{{β_1}•{β_3}}}{{{β_2}•{β_4}}}+…+\frac{{{β_1}•{β_3}•{β_5}…{β_{2n-1}}}}{{{β_2}•{β_4}•{β_6}…{β_{2n}}}}<\sqrt{2{β_n}+1}$-1.
解答 解:(1)将直线l:y=x与椭圆C1:$\frac{{x}^{2}}{2}+{y}^{2}=1$联立得:x1=$\sqrt{\frac{2}{3}}$,
将直线l:y=x与椭圆C2:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$联立得:x2=2$\sqrt{\frac{2}{3}}$,
故α1=|A1A2|=$\sqrt{2}$|x1-x2|=$\sqrt{2}$×$\sqrt{\frac{2}{3}}$=$\frac{2\sqrt{3}}{3}$.
证明:(2)将直线l:y=x与椭圆Cn:$\frac{{x}^{2}}{{2}^{2n-1}}+\frac{{y}^{2}}{{2}^{2n-2}}=1$联立得:xn=2n-1$\sqrt{\frac{2}{3}}$,
则xn+1=2n$\sqrt{\frac{2}{3}}$,
故αn=|AnAn+1|=$\sqrt{2}$|xn-xn+1|=$\sqrt{2}$×2n-1$\sqrt{\frac{2}{3}}$=$\frac{\sqrt{3}•{2}^{n}}{3}$,
即:{αn}为以$\frac{2\sqrt{3}}{3}$为首项,以2为公比的等比数列;
(3)${β_n}={log_2}(\sqrt{3}{α_n})$=$lo{g}_{2}(\sqrt{3}•\frac{\sqrt{3}•{2}^{n}}{3})$=n,
∵$[\frac{1×3×5×…×(2n-1)}{2×4×6×…×2n}]^{2}$=$\frac{1×3}{{2}^{2}}•\frac{3×5}{{4}^{2}}•$…•$\frac{(2n-1)×(2n+1)}{{(2n)}^{2}}$•$\frac{1}{2n+1}$<$\frac{1}{2n+1}$,
故$\frac{1×3×5×…×(2n-1)}{2×4×6×…×2n}$<$\frac{1}{\sqrt{2n+1}}$,
又由$\sqrt{2n+1}$>$\frac{\sqrt{2n+1}+\sqrt{2n-1}}{2}$,
故$\frac{1}{\sqrt{2n+1}}$<$\sqrt{2n+1}-\sqrt{2n-1}$,
∴$\frac{1}{2}$+$\frac{1•3}{2•4}$+…+$\frac{1×3×5×…×(2n-1)}{2×4×6×…×2n}$<$\sum _{k=1}^{n}\frac{1}{\sqrt{2k+1}}$<$\sqrt{2n+1}-1$,
即$\frac{β_1}{β_2}+\frac{{{β_1}•{β_3}}}{{{β_2}•{β_4}}}+…+\frac{{{β_1}•{β_3}•{β_5}…{β_{2n-1}}}}{{{β_2}•{β_4}•{β_6}…{β_{2n}}}}<\sqrt{2{β_n}+1}$-1.
点评 本题考查的知识点是椭圆的简单性质,等比数列,对数的运算性质,放缩法证明不等关系,综合性强,运算量大,转化困难,属于难题.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | (-2,2) | B. | (-2,+∞) | C. | (-2,2] | D. | ∅ |
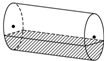 一个水平放置的圆柱形储油桶(如图所示),桶内有油部分所在圆弧占底面圆周长的$\frac{1}{4}$,则油桶直立时,油的高度与桶的高度的比值是$\frac{1}{4}$-$\frac{1}{2π}$.(结果保留π)
一个水平放置的圆柱形储油桶(如图所示),桶内有油部分所在圆弧占底面圆周长的$\frac{1}{4}$,则油桶直立时,油的高度与桶的高度的比值是$\frac{1}{4}$-$\frac{1}{2π}$.(结果保留π)