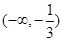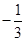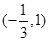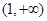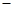题目内容
已知函数 .(
.( ).
).
(1)当 时,求函数
时,求函数 的极值;
的极值;
 (2)若对
(2)若对 ,有成立,求实数
,有成立,求实数 的取值范围.
的取值范围.
【答案】
(1)当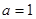 时,
时,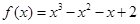 ,
,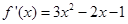 =
=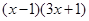 ,
,
令 ,解得
,解得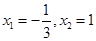 .
.
当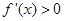 时,得
时,得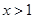 或
或 ;当
;当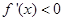 时,得
时,得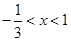 .
.
当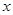 变化时,
变化时,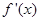 ,
,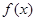 的变化情况如下表: ----------------3分
的变化情况如下表: ----------------3分
|
|
|
|
|
1 |
|
|
|
+ |
0 |
|
0 |
+ |
|
|
单调递增 |
极大 |
单调递减 |
极小 |
单调递增 |
∴当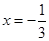 时,函数
时,函数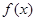 有极大值,
有极大值,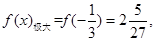 --------------4分
--------------4分
当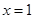 时函数
时函数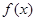 有极小值,
有极小值,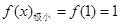 ------------------5分
------------------5分
(2)∵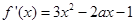 ,∴对
,∴对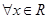 ,
,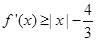 成立,
成立,
即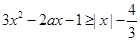 对
对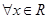 成立,---------------------6分
成立,---------------------6分
①当 时,有
时,有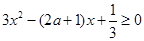 ,即
,即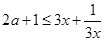 ,对
,对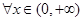 恒成立,
恒成立,
∵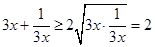 ,当且仅当
,当且仅当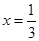 时等号成立,
时等号成立,
∴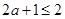
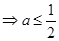 ----------------------------------9分
----------------------------------9分
②当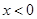 时,有
时,有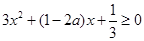 ,即
,即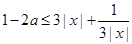 ,对
,对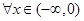 恒成立,
恒成立,
∵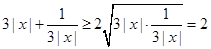 ,当且仅当
,当且仅当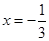 时等号成立,
时等号成立,
∴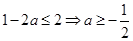 --------------------11分
--------------------11分
③当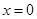 时,
时,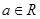 。综上得实数
。综上得实数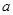 的取值范围为
的取值范围为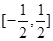 .
.
【解析】略

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|