题目内容
(本小题满分14分)若函数 ,
,
(1)当 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)函数 是否存在极值.
是否存在极值.
解:(1)由题意,函数 的定义域为
的定义域为 ………………2分
………………2分
当 时,
时, ,
, ……3分
……3分
令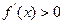 ,即
,即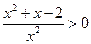 ,得
,得 或
或 ………………5分
………………5分
又因为 ,所以,函数
,所以,函数 的单调增区间为
的单调增区间为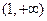 ………………6分
………………6分
(2) ……………7分
……………7分
解法一:令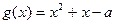 ,因为
,因为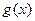 对称轴
对称轴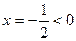 ,所以只需考虑
,所以只需考虑 的正负,
的正负,
当 即
即 时,在(0,+∞)上
时,在(0,+∞)上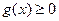 ,
,
即 在(0,+∞)单调递增,
在(0,+∞)单调递增, 无极值 ………………10分
无极值 ………………10分
当 即
即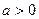 时,
时, 在(0,+∞)有解,所以函数
在(0,+∞)有解,所以函数 存在极值.…
存在极值.… 12分
12分
综上所述:当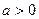 时,函数
时,函数 存在极值;当
存在极值;当 时,函数
时,函数 不存在极值.…14分
不存在极值.…14分
解法二:令 即
即 ,记
,记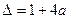
当 即
即
 时,
时,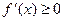 ,
, 在(0,+∞)单调递增,无极值 ………9分
在(0,+∞)单调递增,无极值 ………9分
当 即
即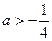 时,解
时,解 得:
得: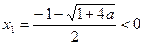 或
或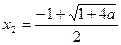
若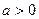 则
则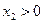 ,列表如下:
,列表如下: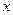
(0, 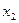 )
)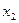
( 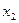 ,+∞)
,+∞)
— 0 + 
↘ 极小值 解析
 练习册系列答案
练习册系列答案
1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
相关题目
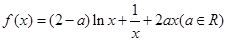
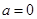 时,求
时,求 的极值
的极值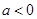 时,求
时,求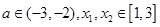 ,恒有
,恒有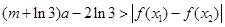 成立,求实数
成立,求实数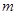 的取值范围。
的取值范围。
 的导数
的导数 ;
; 都有
都有 求a的取值范围。
求a的取值范围。
 .
. 的奇偶性并证明;
的奇偶性并证明; ,证明:函数
,证明:函数 上是增函数.
上是增函数. 分15分)已知函数
分15分)已知函数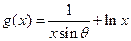 在
在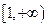 上为增函数,且
上为增函数,且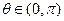 ,
,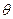 为常数,
为常数,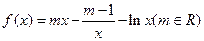 .
.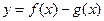 在
在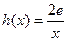 ,若在
,若在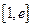 上至少存在一个
上至少存在一个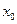 ,使得
,使得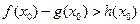 成立,求的m取值范围.
成立,求的m取值范围. 与x=1时都取得极值.
与x=1时都取得极值.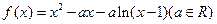 .
.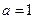 时,求函数
时,求函数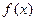 的最值;
的最值;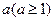 使
使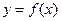 的图象与
的图象与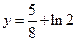 无公共点.
无公共点.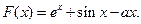
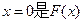 的极值点,求a的值;
的极值点,求a的值;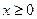 时,函数
时,函数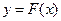 的图象恒不在
的图象恒不在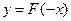 的图象下方,求实数a的取值范围。
的图象下方,求实数a的取值范围。