题目内容
(本小题满分12分)已知函数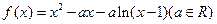 .
.
(1) 当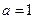 时,求函数
时,求函数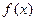 的最值;
的最值;
(2) 求函数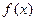 的单调区间;
的单调区间;
(3)(仅385班、389班学生做) 试说明是否存在实数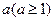 使
使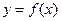 的图象与
的图象与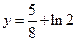 无公共点.
无公共点.
解:(1) 函数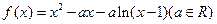 的定义域是
的定义域是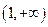 .
.
当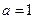 时,
时,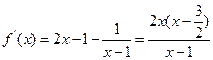 ,所以
,所以 在
在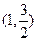 为减函数 ,
为减函数 ,
在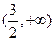 为增函数,所以函数f (x)的最小值为
为增函数,所以函数f (x)的最小值为 =
= .
.
(2) 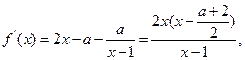
若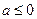 时,则
时,则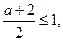 f(x)
f(x)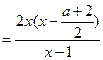
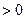 在
在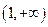 恒成立,
恒成立,
所以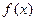 的增区间为
的增区间为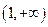 .
.
若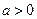 ,则
,则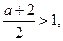 故当
故当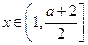 ,
,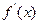
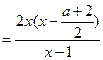
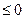 ,
,
当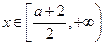 时,f(x)
时,f(x)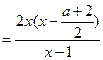
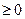 ,
,
所以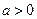 时
时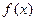 的减区间为
的减区间为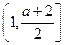 ,
,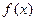 的增区间为
的增区间为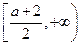 .
.
(3)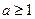 时,由(1)知
时,由(1)知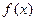 在
在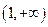 上的最小值为
上的最小值为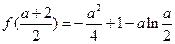 ,
,
令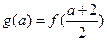
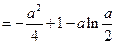 在
在 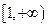 上单调递减,
上单调递减,
所以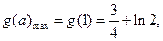 则
则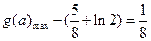
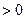 ,
,
因此存在实数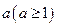 使
使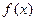 的最小值大于
的最小值大于 ,
,
故存在实数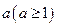 使
使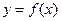 的图象与
的图象与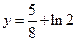 无公共点.
无公共点.
解析

练习册系列答案
相关题目
 的单调递减区间;
的单调递减区间; , x∈[-1, b](b > -1),在x = -1处取得最小值,试求b的最大值.
, x∈[-1, b](b > -1),在x = -1处取得最小值,试求b的最大值. (e为自然对数的底)。
(e为自然对数的底)。 在其定义域为单调函数,求p的取值范围。
在其定义域为单调函数,求p的取值范围。 。
。
 ;
; .若直线
.若直线 1、
1、 的图象以及
的图象以及
 、b、c的值;
、b、c的值; 问是否存在实数m,使得
问是否存在实数m,使得 的图象与
的图象与 的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
 资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元. 的费用为y(元)(不计返程费用),将y表示成速度v的函数
的费用为y(元)(不计返程费用),将y表示成速度v的函数 关系式;
关系式;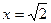 是函数
是函数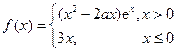 的极值点.
的极值点.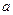 的值;
的值; 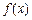 的单调区间;
的单调区间;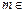 R时,试讨论方程
R时,试讨论方程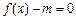 的解的个数.
的解的个数. =_________.
=_________. ,
, 时,求函数
时,求函数 的单调增区间;
的单调增区间; 函数
函数 在
在 处取得极值.
处取得极值. ;
; ,如果
,如果 在开区间
在开区间 上存在极小值,求实数
上存在极小值,求实数 的取值范围.
的取值范围.