题目内容
8．在△ABC中，AB=3，AC=$\sqrt{10}$，BC=2，则$\overrightarrow{AB}$•$\overrightarrow{BC}$=-$\frac{3}{2}$．分析 运用余弦定理可得cosB，再由向量的数量积的定义，即可得到所求．
解答 解：由余弦定理可得，
cosB=$\frac{{3}^{2}+{2}^{2}-（\sqrt{10}）^{2}}{2×3×2}$=$\frac{1}{4}$，
则$\overrightarrow{AB}$•$\overrightarrow{BC}$=3×2cos（π-B）=-6cosB
=-6×$\frac{1}{4}$=-$\frac{3}{2}$．
故答案为：-$\frac{3}{2}$．
点评 本题考查余弦定理的运用，向量的数量积的定义，注意向量的夹角的概念，属于基础题．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
16．
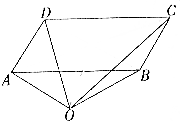如图所示，平行四边形ABCD中，O为平面内任一点，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，$\overrightarrow{OD}$=$\overrightarrow{d}$，则（ ）
如图所示，平行四边形ABCD中，O为平面内任一点，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，$\overrightarrow{OD}$=$\overrightarrow{d}$，则（ ）| A． | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$+$\overrightarrow{d}$=$\overrightarrow{0}$ | B． | $\overrightarrow{a}$-$\overrightarrow{b}$-$\overrightarrow{c}$-$\overrightarrow{d}$=$\overrightarrow{0}$ | C． | $\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$-$\overrightarrow{d}$=$\overrightarrow{0}$ | D． | $\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$-$\overrightarrow{d}$=$\overrightarrow{0}$ |