题目内容
在计算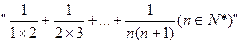 时,某同学学到了如下一种方法:
时,某同学学到了如下一种方法:
先改写第K项:
由此得
相加,得
类比上述方法,请计算 ,其结果为___________.
,其结果为___________.
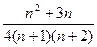
解析

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
题目内容
在计算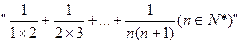 时,某同学学到了如下一种方法:
时,某同学学到了如下一种方法:
先改写第K项:
由此得
相加,得
类比上述方法,请计算 ,其结果为___________.
,其结果为___________.
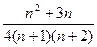
解析

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案