题目内容
已知:函数y=f(x),x∈R,满足f(1)=2,f(x+y)=f(x)*f(y),且f(x)是增函数,
(1)证明:f(0)=1;
(2)若f(2x)*f(x2-1)≥4成立,求x的取值范围.
(1)证明:f(0)=1;
(2)若f(2x)*f(x2-1)≥4成立,求x的取值范围.
(1)由题意可令x=y=0,代入f(x+y)=f(x)×f(y),得f(0)=f(0)*f(0),
解得f(0)=0或f(0)=1,
若f(0)=0,令x=1,y=0,则有f(1+0)=f(1)×f(0)=0,这与f(1)=2矛盾,故 f(0)=1
(2)由题意f(2x)×f(x2-1)≥4可变为f(x2-1+2x)≥4=2×2=f(1)×f(1)=f(2),
又f(x)是增函数
故有x2-1+2x≥2,整理得x2-3+2x≥0
解得x≥1或x≤-3
所以x的取值范围是x≥1或x≤-3
解得f(0)=0或f(0)=1,
若f(0)=0,令x=1,y=0,则有f(1+0)=f(1)×f(0)=0,这与f(1)=2矛盾,故 f(0)=1
(2)由题意f(2x)×f(x2-1)≥4可变为f(x2-1+2x)≥4=2×2=f(1)×f(1)=f(2),
又f(x)是增函数
故有x2-1+2x≥2,整理得x2-3+2x≥0
解得x≥1或x≤-3
所以x的取值范围是x≥1或x≤-3

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
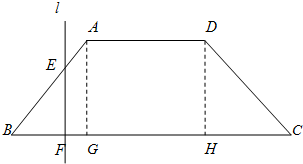
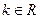 ,函数
,函数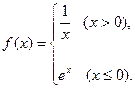 ,
,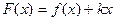 ,
,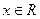 .
.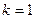 时,求
时,求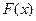 的值域;
的值域;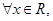
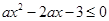 恒成立”是真命题,则实数a的取值范围是 .
恒成立”是真命题,则实数a的取值范围是 .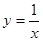 (x>0)图像上一动点,若点P,A之间的最短距离为
(x>0)图像上一动点,若点P,A之间的最短距离为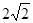 ,则满足条件的实数a所有值为_________.
,则满足条件的实数a所有值为_________.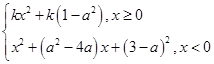 ,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则实数k的取值范围是________.
,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则实数k的取值范围是________.