题目内容
(本题满分15分)
已知点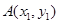 ,
, 是抛物线
是抛物线 上相异两点,且满足
上相异两点,且满足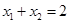 .
.
(Ⅰ)若 的中垂线经过点
的中垂线经过点 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)若 的中垂线交
的中垂线交 轴于点
轴于点 ,求
,求 的面积的最大值及此时直线
的面积的最大值及此时直线 的方程.
的方程.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)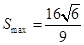 ,直线
,直线 方程为
方程为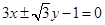 。
。
解析试题分析:(I)当 垂直于
垂直于 轴时,显然不符合题意,
轴时,显然不符合题意,
所以可设直线 的方程为
的方程为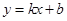 ,代入方程
,代入方程 得:
得: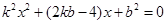
∴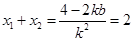 ………………………………2分
………………………………2分
得: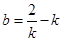
∴直线 的方程为
的方程为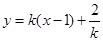
∵ 中点的横坐标为1,∴
中点的横坐标为1,∴ 中点的坐标为
中点的坐标为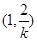 …………………………4分
…………………………4分
∴ 的中垂线方程为
的中垂线方程为
∵ 的中垂线经过点
的中垂线经过点 ,故
,故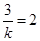 ,得
,得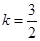 ………………………6分
………………………6分
∴直线 的方程为
的方程为 ………………………7分
………………………7分
(Ⅱ)由(I)可知 的中垂线方程为
的中垂线方程为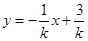 ,∴
,∴ 点的坐标为
点的坐标为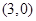 ……8分
……8分
因为直线 的方程为
的方程为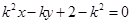
∴ 到直线
到直线 的距离
的距离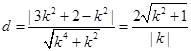 …………………10分
…………………10分
由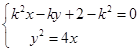 得,
得,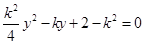 ,
,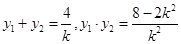
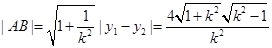 …………………………12分
…………………………12分
∴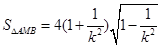 , 设
, 设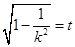 ,则
,则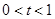 ,
,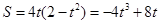 ,
,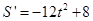 ,由
,由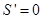 ,得
,得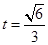
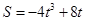 在
在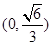 上递增,在
上递增,在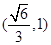 上递减,当
上递减,当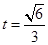 时,
时,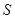 有最大值
有最大值
得: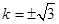 时,
时,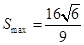
直线 方程为
方程为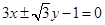 ……………15分
……………15分
(本题若运用基本不等式解决,也同样给分)
法二:
(Ⅰ)当 垂直于
垂直于 轴时,显然不符合题意,
轴时,显然不符合题意,
当 不垂直于
不垂直于 轴时,根据题意设
轴时,根据题意设 的中点为
的中点为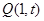 ,
,
则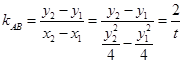 &nbs
&nbs

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系xoy的原点为极点,OX为极轴,且长度单位相同,建立极坐标系,直线l的极坐标方程为 ρsin(θ+)="0," 求与直线l垂直且与曲线C相切的直线m的极坐标方程.
为参数),若以直角坐标系xoy的原点为极点,OX为极轴,且长度单位相同,建立极坐标系,直线l的极坐标方程为 ρsin(θ+)="0," 求与直线l垂直且与曲线C相切的直线m的极坐标方程. :
:
 取何值,直线
取何值,直线
 和四边形
和四边形 的面积满足
的面积满足 时,请你确定P点在AB上的位置,并求出线段PQ的长;
时,请你确定P点在AB上的位置,并求出线段PQ的长; 与
与 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 中,已知BC边上的高所在直线的方程为
中,已知BC边上的高所在直线的方程为 ,
, 平分线所在直线的方程为
平分线所在直线的方程为 ,若点B的坐标为(1,2),
,若点B的坐标为(1,2),