题目内容
(本题满分12分)在 中,已知BC边上的高所在直线的方程为
中,已知BC边上的高所在直线的方程为 ,
, 平分线所在直线的方程为
平分线所在直线的方程为 ,若点B的坐标为(1,2),
,若点B的坐标为(1,2),
(Ⅰ)求直线BC的方程;
(Ⅱ)求点C的坐标。
(Ⅰ)2x+y-4=0(Ⅱ)C(5,-6)
解析试题分析:(Ⅰ).因为BC与BC边上的高互相垂直,且BC边上的高的斜率为 1/2 ,所以,直线BC的斜率为 -2 ,
因此由点斜式可得直线BC的方程为 y-2="-2(x-1)" ,化简得 2x+y-4="0" 。
(Ⅱ)由x-2y+1=0和y=0求得A(-1, 0)
由AB,AC关于角A平分线x轴对称的AC直线方程y="-x-1"
由 于BC方程为:y="-2x+4" 由BC,AC联立解得C(5,-6)
考点:直线方程及直线的位置关系
点评:角的两条边关于角平分线是对称的

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 的方程为3x+4y-12=0,求满足下列条件的直线
的方程为3x+4y-12=0,求满足下列条件的直线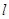 的方程.
的方程.

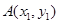 ,
, 是抛物线
是抛物线 上相异两点,且满足
上相异两点,且满足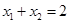 .
. 的中垂线经过点
的中垂线经过点 ,求直线
,求直线 轴于点
轴于点 ,求
,求 的面积的最大值及此时直线
的面积的最大值及此时直线 的最小值.
的最小值. 、
、 ,使
,使 ,
,
 .
. 的轨迹
的轨迹 的方程;
的方程; 上任取一点
上任取一点 做曲线
做曲线 、
、 ,求证:直线
,求证:直线 恒过一定点.
恒过一定点.
 满足圆的标准方程
满足圆的标准方程 ,
, 的最小值;
的最小值; 到圆上点的最大值.
到圆上点的最大值. x+1的倾斜角的
x+1的倾斜角的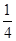 ,且分别满足下列条件的直线方程:
,且分别满足下列条件的直线方程:  的直线方程;
的直线方程;