ЬтФПФкШн
ЁОЬтФПЁПвбжЊЕШБШЪ§Са{![]() }ЕФЧАnЯюКЭЮЊ
}ЕФЧАnЯюКЭЮЊ![]() ЃЌЧвТњзу2
ЃЌЧвТњзу2![]() ЃН
ЃН![]() ЃЋmЃЈmЁЪRЃЉЃЎ
ЃЋmЃЈmЁЪRЃЉЃЎ
ЃЈЂёЃЉЧѓЪ§Са{![]() }ЕФЭЈЯюЙЋЪНЃЛ
}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈЂђЃЉШєЪ§Са{![]() }Тњзу
}Тњзу![]() ЃЌЧѓЪ§Са{
ЃЌЧѓЪ§Са{![]() }ЕФЧАnЯюКЭ
}ЕФЧАnЯюКЭ![]() ЃЎ
ЃЎ
ЁОД№АИЁПЃЈЂёЃЉ![]() ЃЈЂђЃЉ
ЃЈЂђЃЉ![]()
ЁОНтЮіЁП
(Ђё)ЗЈвЛЃКгЩЧАnЯюКЭгыЪ§СаЭЈЯюЙЋЪНЕФЙиЯЕПЩЕУЪ§СаЕФЭЈЯюЙЋЪНЮЊ![]() ЃЛ
ЃЛ
ЗЈЖўЃКгЩЬтвтПЩЕУ ЃЌдђ
ЃЌдђ![]() ЃЌОнДЫПЩЕУЪ§СаЕФЭЈЯюЙЋЪНЮЊ
ЃЌОнДЫПЩЕУЪ§СаЕФЭЈЯюЙЋЪНЮЊ![]() .
.
ЃЈЂђЃЉгЩЃЈЂёЃЉПЩЕУ![]() ЃЌСбЯюЧѓКЭПЩЕУ
ЃЌСбЯюЧѓКЭПЩЕУ![]() .
.
(Ђё)ЗЈвЛЃК
гЩ![]() ЕУ
ЕУ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
гж![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЗћКЯЩЯЪНЃЌЫљвдЭЈЯюЙЋЪНЮЊ
ЪБЗћКЯЩЯЪНЃЌЫљвдЭЈЯюЙЋЪНЮЊ![]() .
.
ЗЈЖўЃК
гЩ![]() ЕУ
ЕУ
ДгЖјга![]() ЃЌ
ЃЌ
ЫљвдЕШБШЪ§СаЙЋБШ![]() ЃЌЪзЯю
ЃЌЪзЯю![]() ЃЌвђДЫЭЈЯюЙЋЪНЮЊ
ЃЌвђДЫЭЈЯюЙЋЪНЮЊ![]() .
.
ЃЈЂђЃЉгЩЃЈЂёЃЉПЩЕУ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() .
.
ЁОЕуОІЁП
БОЬтжївЊПМВщЪ§СаЧАnЯюКЭгыЭЈЯюЙЋЪНЕФЙиЯЕЃЌСбЯюЧѓКЭЕФЗНЗЈЕШжЊЪЖЃЌвтдкПМВщбЇЩњЕФзЊЛЏФмСІКЭМЦЫуЧѓНтФмСІ.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
18
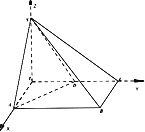
ЁОЬтФПЁПЫФРтзЖSЃABCDЕФЕзУцABCDЮЊжБНЧЬнаЮЃЌABЁЮCDЃЌABЁЭBCЃЌABЃН2BCЃН2CDЃН2ЃЌЁїSADЮЊе§Ш§НЧаЮЃЎ
ЃЈЂёЃЉЕуMЮЊРтABЩЯвЛЕуЃЌШєBCЁЮЦНУцSDMЃЌAMЃНІЫABЃЌЧѓЪЕЪ§ІЫЕФжЕЃЛ
ЃЈЂђЃЉШєBCЁЭSDЃЌЧѓЖўУцНЧAЃSBЃCЕФгрЯвжЕЃЎ

ЁОД№АИЁПЃЈЂёЃЉ![]() ЃЈЂђЃЉ
ЃЈЂђЃЉ![]()
ЁОНтЮіЁП
ЃЈЂёЃЉгЩЯпУцЦНааЕФаджЪЖЈРэПЩЕУ![]() ЃЌОнДЫПЩжЊЫФБпаЮBCDMЮЊЦНааЫФБпаЮЃЌОнДЫПЩЕУ
ЃЌОнДЫПЩжЊЫФБпаЮBCDMЮЊЦНааЫФБпаЮЃЌОнДЫПЩЕУ![]() .
.
ЃЈЂђЃЉгЩМИКЮЙиЯЕЃЌдкЦНУц![]() ФкЙ§Еу
ФкЙ§Еу![]() зї
зї![]() жБЯп
жБЯп![]() гкЕу
гкЕу![]() ЃЌвдЕуEЮЊзјБъдЕуЃЌEAЗНЯђЮЊXжсЃЌECЗНЯђЮЊYжсЃЌESЗНЯђЮЊZжсНЈСЂПеМфзјБъЯЕЃЌОнДЫПЩЕУЦНУц
ЃЌвдЕуEЮЊзјБъдЕуЃЌEAЗНЯђЮЊXжсЃЌECЗНЯђЮЊYжсЃЌESЗНЯђЮЊZжсНЈСЂПеМфзјБъЯЕЃЌОнДЫПЩЕУЦНУц![]() ЕФвЛИіЗЈЯђСП
ЕФвЛИіЗЈЯђСП![]() ЃЌЦНУц
ЃЌЦНУц![]() ЕФвЛИіЗЈЯђСП
ЕФвЛИіЗЈЯђСП![]() ЃЌОнДЫМЦЫуПЩЕУЖўУцНЧ
ЃЌОнДЫМЦЫуПЩЕУЖўУцНЧ![]() грЯвжЕЮЊ
грЯвжЕЮЊ![]() .
.
ЃЈЂёЃЉвђЮЊ![]() ЦНУцSDM,
ЦНУцSDM,![]()
![]() ЦНУцABCD,ЦНУцSDM
ЦНУцABCD,ЦНУцSDM ![]() ЦНУцABCD=DM,Ыљвд
ЦНУцABCD=DM,Ыљвд![]() ЃЌ
ЃЌ
вђЮЊ![]() ,ЫљвдЫФБпаЮBCDMЮЊЦНааЫФБпаЮЃЌгж
,ЫљвдЫФБпаЮBCDMЮЊЦНааЫФБпаЮЃЌгж![]() ,ЫљвдMЮЊABЕФжаЕу.
,ЫљвдMЮЊABЕФжаЕу.
вђЮЊ![]()
![]() .
.
ЃЈЂђЃЉвђЮЊ![]()
![]() ЃЌ
ЃЌ ![]()
![]() ЃЌЫљвд
ЃЌЫљвд![]() ЦНУц
ЦНУц![]() ЃЌгжвђЮЊ
ЃЌгжвђЮЊ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ
ЫљвдЦНУц![]() ЦНУц
ЦНУц![]() ЃЌЦНУц
ЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ
дкЦНУц![]() ФкЙ§Еу
ФкЙ§Еу![]() зї
зї![]() жБЯп
жБЯп![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ
дк![]() КЭ
КЭ![]() жаЃЌвђЮЊ
жаЃЌвђЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
гжгЩЬтжЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() Ыљвд
Ыљвд![]() ЃЌ
ЃЌ
вдЯТНЈЯЕЧѓНт.вдЕуEЮЊзјБъдЕуЃЌEAЗНЯђЮЊXжсЃЌECЗНЯђЮЊYжсЃЌESЗНЯђЮЊZжсНЈСЂШчЭМЫљЪОПеМфзјБъЯЕЃЌ
дђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЩшЦНУц![]() ЕФЗЈЯђСП
ЕФЗЈЯђСП![]() ЃЌдђ
ЃЌдђ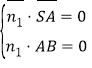 ЃЌЫљ
ЃЌЫљ![]() ЃЌ
ЃЌ
Сю![]() ЕУ
ЕУ![]() ЮЊЦНУц
ЮЊЦНУц![]() ЕФвЛИіЗЈЯђСПЃЌ
ЕФвЛИіЗЈЯђСПЃЌ
ЭЌРэЕУ![]() ЮЊЦНУц
ЮЊЦНУц![]() ЕФвЛИіЗЈЯђСПЃЌ
ЕФвЛИіЗЈЯђСПЃЌ
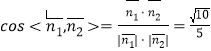 ЃЌвђЮЊЖўУцНЧ
ЃЌвђЮЊЖўУцНЧ![]() ЮЊЖлНЧ.
ЮЊЖлНЧ.
ЫљвдЖўУцНЧ![]() грЯвжЕЮЊ
грЯвжЕЮЊ![]() .
.

