题目内容
【题目】如图,在三棱锥S﹣ABC中,SB⊥底面ABC,且SB=AB=2,BC= ![]() ,D、E分别是SA、SC的中点.
,D、E分别是SA、SC的中点.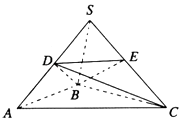
(I)求证:平面ACD⊥平面BCD;
(II)求二面角S﹣BD﹣E的平面角的大小.
【答案】证明:(I)∵∠ABC= ![]() ,
,
∴BA⊥BC,
建立如图所示的坐标系,
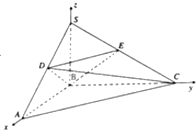
则C(0, ![]() ,0),A(2,0,0),D(1,0,1),E(0,
,0),A(2,0,0),D(1,0,1),E(0, ![]() ,1),S(0,0,2),
,1),S(0,0,2),
则 ![]() =(﹣1,0,1),
=(﹣1,0,1), ![]() =(0,
=(0, ![]() ,0),
,0),
![]() =(1,0,1),
=(1,0,1),
则 ![]()
![]() =(﹣1,0,1)(0,
=(﹣1,0,1)(0, ![]() ,0)=0,
,0)=0,
![]()
![]() =(﹣1,0,1)(1,0,1)=﹣1+1=0,
=(﹣1,0,1)(1,0,1)=﹣1+1=0,
则 ![]() ⊥
⊥ ![]() ,
, ![]() ⊥
⊥ ![]() ,
,
即AD⊥BC,AD⊥BD,
∵BC∩BD=B,
∴AD⊥平面BCD;
∵AD平面BCD;
∴平面ACD⊥平面BCD;
(II) ![]() =(0,
=(0, ![]() ,1),
,1),
则设平面BDE的法向量 ![]() =(x,y,1),
=(x,y,1),
则 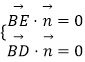 ,即
,即 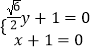 ,
,
解得x=﹣1,y= ![]() ,
,
即 ![]() =(﹣1,
=(﹣1, ![]() ,1),
,1),
又平面SBD的法向量 ![]() =(0,
=(0, ![]() ,0),
,0),
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
则< ![]() ,
, ![]() >=
>= ![]() ,即二面角S﹣BD﹣E的平面角的大小为
,即二面角S﹣BD﹣E的平面角的大小为 ![]() .
.
【解析】(1)欲证明平面ACD⊥平面BCD,根据面面垂直的判定定理,证明AD⊥平面BCD。欲证明AD⊥平面BCD,根据线面垂直的判定定理,证明AD⊥BC,AD⊥BD即可证明。
(2)设平面BDE的法向量 ![]() =(x,y,1),利用向量的数量积公式即可求得。
=(x,y,1),利用向量的数量积公式即可求得。
【考点精析】认真审题,首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直).

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目