��Ŀ����
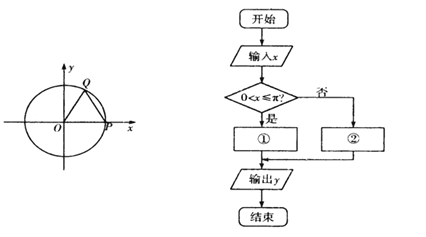
����Ŀ����ͼ,��֪��λԲx2+y2=1��x�������ύ�ڵ�P,��Բ��һ����Q��P��������ʱ�뷽����תһ�ܻص�P���ֹͣ�˶���OQɨ�������ζ�Ӧ��Բ�Ľ�Ϊxrad,��0<x<2��ʱ,��Բ��O��ֱ��PQ�ľ���Ϊy,y��x�ĺ�����ϵʽy=f(x)����ͼ��ʾ�ij����ͼ�еĢ٢�������ϵʽ
(��)д�������ͼ�Т٢ڴ��ĺ�����ϵʽ;
(��)�������yֵΪ2,���Q������.
���𰸡�(1)������;(2)������.
�������������������1����������õ���������ʽΪf(x)= ��������һ�����ɵõ��������2����0<x<2
��������һ�����ɵõ��������2����0<x<2![]() ʱx=
ʱx=![]() ��
��![]() <x<2
<x<2![]() ʱ, x=
ʱ, x=![]() ���ֱ���õ������.
���ֱ���õ������.
������
(I)��0<x�ܦ�ʱ,y=cos![]() ;,
;,
����<x<2��ʱ,y=cos(��-![]() )=-cos
)=-cos![]()
���Ͽ�֪,��������ʽΪf(x)= .
.
���Կ�ͼ�Т٢ڴ�Ӧ����ʽ�ӷֱ�Ϊy=cos![]() ,y=-cos
,y=-cos![]() ,
,
(��)�������yֵΪ,��
��0<x<2![]() ʱ��cos
ʱ��cos![]() =
=![]() ,��x=
,��x=![]() ,��ʱ��Q������Ϊ(-
,��ʱ��Q������Ϊ(-![]() ,
,![]() ;
;
��![]() <x<2
<x<2![]() ʱ,��-cos=
ʱ,��-cos=![]() =
=![]() ,��x=
,��x=![]() ,��ʱ��Q������Ϊ(-
,��ʱ��Q������Ϊ(-![]() ,-
,-![]() ).
).

��ϰ��ϵ�д�
 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
�����Ŀ