题目内容
(本小题满分 14分)
14分)
已知各项均为正数的数列{an}前n项和为Sn,(p – 1)Sn = p2 – an,n ∈N*,p > 0且p≠1,数列{bn}满足bn = 2logpan.
(Ⅰ)若p =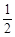 ,设数列
,设数列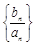 的前n项和为Tn,求证:0 < Tn≤4;
的前n项和为Tn,求证:0 < Tn≤4;
(Ⅱ)是否存在自然数M,使得当n > M时,an > 1恒成立?若存在,求出相应的M;若不存在, 请说明理由.
请说明理由.
(Ⅰ)解:由(p – 1)Sn = p2 – an (n∈N*) ①
由(p – 1)Sn
– 1 = p 2 – an – 1 ②
2 – an – 1 ②
① – ②得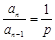 (n≥2)
(n≥2)
∵an > 0 (n∈N*)
又(p
– 1)S1 = p2 – a 1,∴a1 = p
1,∴a1 = p
{an}是以p为首项,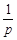 为公比的等比数列
为公比的等比数列
an = p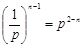
bn = 2logpan = 2logpp2 – n
∴bn = 4 – 2n ………… 4分
证明:由条件p =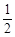 得an = 2n – 2
得an = 2n – 2
∴Tn =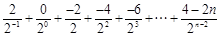 ①
①
 ②
②
① – ②得
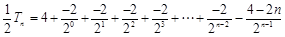
= 4 – 2 ×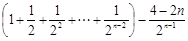 [来源:Z|xx|k.Com]
[来源:Z|xx|k.Com]
= 4 – 2 ×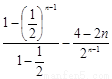
∴Tn =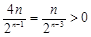 ………… 8分
………… 8分
Tn – Tn – 1 =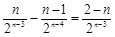
当n > 2时,Tn – Tn – 1< 0
所以,当n > 2时,0 < Tn≤T3 = 3
又T1 = T2 = 4,∴0 < Tn≤4.…………10分
(Ⅱ)解:若要使an > 1恒成立,则需分p > 1和0 < p < 1两种情况讨论
当p > 1时,2 – n > 0,n < 2
当0 < p < 1时,2 – n < 0,n > 2
 ∴当0 < p < 1时,存在M = 2
∴当0 < p < 1时,存在M = 2
当n > M时,an > 1恒成立.………… 14分
【解析】略

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)