题目内容
【题目】已知数列{an}满足:a1=1,an= 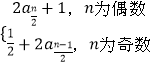 ,n=2,3,4,….
,n=2,3,4,….
(1)求a2 , a3 , a4 , a5的值;
(2)设bn= ![]() +1,n∈N*,求证:数列{bn}是等比数列,并求出其通项公式;
+1,n∈N*,求证:数列{bn}是等比数列,并求出其通项公式;
(3)对任意的m≥2,m∈N*,在数列{an}中是否存在连续的2m项构成等差数列?若存在,写出这2m项,并证明这2m项构成等差数列;若不存在,请说明理由.
【答案】
(1)解:∵a1=1,∴a2=1+2a1=3,
a3= ![]() +2a2=
+2a2= ![]() ,
,
a4=1+2a3=7,
a5= ![]() +2a4=
+2a4= ![]()
(2)解:由题意,对于任意的正整数n,bn= ![]() +1,
+1,
∴bn+1= ![]() +1,
+1,
又∵ ![]() +1=(2
+1=(2 ![]() +1)+1=2(
+1)+1=2( ![]() +1)=2bn,
+1)=2bn,
∴bn+1=2bn,
又∵b1= ![]() +1=a1+1=2,
+1=a1+1=2,
∴数列{bn}是首项、公比均为2的等比数列,其通项公式bn=2n
(3)解:对任意的m≥2,m∈N*,在数列{an}中存在连续的2m项构成等差数列.
对任意的m≥2,k∈N*,在数列{an}中, ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 这连续的2m就构成一个等差数列.
这连续的2m就构成一个等差数列.
我们先来证明:“对任意的n≥2,n∈N*,k∈(0,2n﹣1),k∈N*,有 ![]() ”,
”,
由(2)得 ![]() ,∴
,∴ ![]() ,
,
当k为奇数时, ![]() =
= ![]() ,
,
当k为偶数时, ![]() =1+2a
=1+2a ![]() ,
,
记 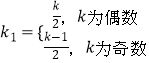 ,∴要证
,∴要证 ![]() =
= ![]() ,只需证明
,只需证明 ![]() ,
,
其中 ![]() ,k1∈N*,
,k1∈N*,
(这是因为若 ![]() ,则当
,则当 ![]() 时,则k一定是奇数)
时,则k一定是奇数)
有 ![]() =
= ![]()
= ![]() =
= ![]() ,
,
当 ![]() 时,则k一定是偶数,
时,则k一定是偶数,
有 ![]() =1+
=1+ ![]()
=1+2( ![]() )=1+2(
)=1+2( ![]() )=
)= ![]() ,
,
以此递推,要证 ![]() =
= ![]() ,只要证明
,只要证明 ![]() ,
,
其中 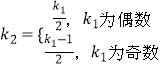 ,k2∈N*,
,k2∈N*,
如此递推下去,我们只需证明 ![]() ,
, ![]() ,
,
即 ![]() ,即
,即 ![]() ,
,
由(Ⅱ)可得,所以对n≥2,n∈N*,k∈(0,2n﹣1),k∈N*,
有 ![]() ,
,
对任意的m≥2,m∈N*,
![]() =
= ![]() ,
, ![]() ,其中i∈(0,2m﹣1),i∈N*,
,其中i∈(0,2m﹣1),i∈N*,
∴ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ,
,
又 ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 这连续的2m项,是首项为
这连续的2m项,是首项为 ![]() ,公差为﹣
,公差为﹣ ![]() 的等差数列
的等差数列
【解析】(1)由a1=1,利用递推公式能求出a2 , a3 , a4 , a5的值.(2)由题意,对于任意的正整数n,bn= ![]() +1,从而bn+1=
+1,从而bn+1= ![]() +1,进而bn+1=2bn , 由此能证明数列{bn}是首项、公比均为2的等比数列,并求出其通项公式.(3)对任意的m≥2,m∈N*,在数列{an}中存在连续的2m项构成等差数列.对任意的m≥2,k∈N* , 在数列{an}中,
+1,进而bn+1=2bn , 由此能证明数列{bn}是首项、公比均为2的等比数列,并求出其通项公式.(3)对任意的m≥2,m∈N*,在数列{an}中存在连续的2m项构成等差数列.对任意的m≥2,k∈N* , 在数列{an}中, ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 这连续的2m就构成一个等差数列.利用构造法和分类讨论法能推导出
这连续的2m就构成一个等差数列.利用构造法和分类讨论法能推导出 ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 这连续的2m项,是首项为
这连续的2m项,是首项为 ![]() ,公差为﹣
,公差为﹣ ![]() 的等差数列.
的等差数列.
【考点精析】本题主要考查了数列的通项公式的相关知识点,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案