题目内容
【题目】设数列{an}各项为正数，且a2=4a1 ， an+1= 
+2an（n∈N*）
（I）证明：数列{log3（1+an）}为等比数列；
（Ⅱ）令bn=log3（1+a2n﹣1），数列{bn}的前n项和为Tn ， 求使Tn＞345成立时n的最小值．
【答案】（I）证明：∵a2=4a1 ， an+1= 
+2an（n∈N*），∴a2=4a1 ， a2= 
，解得a1=2，a2=8．
∴an+1+1= +2an+1= 
，
两边取对数可得：log3（1+an+1）=2log3（1+an），
∴数列{log3（1+an）}为等比数列，首项为1，公比为2．
（II）解：由（I）可得：log3（1+an）=2n﹣1 ，
∴bn=log3（1+a2n﹣1）=22n﹣2=4n﹣1 ，
∴数列{bn}的前n项和为Tn= 
= 
．
不等式Tn＞345，
化为 ＞345，即4n＞1036．
解得n＞5．
∴使Tn＞345成立时n的最小值为6
【解析】（I）由a2=4a1 ， an+1= 
+2an（n∈N*），可得a2=4a1 ， a2= 
，解得a1 ， a2 ． 由于an+1+1= +2an+1= 
，两边取对数可得：log3（1+an+1）=2log3（1+an），即可证明．（II）由（I）可得：log3（1+an）=2n﹣1 ， 可得bn=log3（1+a2n﹣1）=22n﹣2=4n﹣1 ， 可得数列{bn}的前n项和为Tn ， 代入化简即可得出．
【考点精析】根据题目的已知条件，利用等比数列的通项公式（及其变式）和数列的前n项和的相关知识可以得到问题的答案，需要掌握通项公式：
；数列{an}的前n项和sn与通项an的关系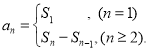
．
【题目】已知数列{an}是公差为2的等差数列，数列{bn}满足 
，若n∈N*时，anbn+1﹣bn+1=nbn ．
（Ⅰ）求{bn}的通项公式；
（Ⅱ）设cn=anbn ， 求{cn}的前n项和Sn ．
【题目】为了解市民在购买食物时看营养说明与性别的关系，现在社会上随机询问了100名市民，得到如下2×2列联表：
（1）是否有95%的把握认为：“性别与读营养说明有关系”，并说明理由；
（2）把频率当概率，若从社会上的男性市民中随机抽取3位，记这3位中读营养说明的人数为ξ，求随机变量ξ的分布列和数学期望E（ξ）．
男性 | 女性 | 总计 | |
读营养说明 | 40 | 20 | 60 |
不读营养说明 | 20 | 20 | 40 |
总计 | 60 | 40 | 100 |
参考公式和数据： 
P（K2≥k0） | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
