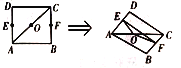题目内容
【题目】已知![]() 的顶点
的顶点![]() 边上的中线
边上的中线![]() 所在直线方程为
所在直线方程为![]() ,
,![]() 边上的高所在直线的方程为
边上的高所在直线的方程为![]() .
.
(1)求![]() 的顶点
的顶点![]() 的坐标;
的坐标;
(2)若圆![]() 经过不同三点
经过不同三点![]() ,且斜率为
,且斜率为![]() 的直线与圆
的直线与圆![]() 相切与点
相切与点![]() ,求圆的方程
,求圆的方程![]() .
.
【答案】(1)![]() ,
,![]() ; (2)圆方程为
; (2)圆方程为![]()
【解析】试题分析:(1)依题意知,点C是直线x=0和![]() 的交点,从而得出点C的坐标;设出点B的坐标由AB的中点在直线CD上求出点B的坐标.(2)线段AB和线段BP是圆的两条弦,所以两条弦的中垂线交点为圆心M坐标,即用m表示圆心M坐标,然后利用点P处的切线的斜率为1,可知
的交点,从而得出点C的坐标;设出点B的坐标由AB的中点在直线CD上求出点B的坐标.(2)线段AB和线段BP是圆的两条弦,所以两条弦的中垂线交点为圆心M坐标,即用m表示圆心M坐标,然后利用点P处的切线的斜率为1,可知![]() ,从而求出m的值,进而求出圆的方程.
,从而求出m的值,进而求出圆的方程.
试题解析:(1)![]() 边上的高
边上的高![]() 所在直线的方程为
所在直线的方程为![]() ,所以,
,所以,![]() ,
,
又![]() ,所以,
,所以,![]() ,
,
设![]() ,则
,则![]() 的中点
的中点![]() ,代入方程
,代入方程![]() ,
,
解得![]() ,所以
,所以![]() .
.
(2)由![]() ,
,![]() 可得,圆
可得,圆![]() 的弦
的弦![]() 的中垂线方程为
的中垂线方程为![]() ,
,
注意到![]() 也是圆
也是圆![]() 的弦,所以,圆心在直线
的弦,所以,圆心在直线![]() 上,
上,
设圆心![]() 坐标为
坐标为![]() ,
,
因为圆心![]() 在直线
在直线![]() 上,所以
上,所以![]() ①,
①,
又因为斜率为![]() 的直线与圆
的直线与圆![]() 相切于点
相切于点![]() ,所以
,所以![]() ,
,
即![]() ,整理得
,整理得![]() ②,
②,
由①②解得![]() ,
,![]() ,
,
所以,![]() ,半径
,半径![]() ,
,
所以所求圆方程为![]() .
.

练习册系列答案
相关题目
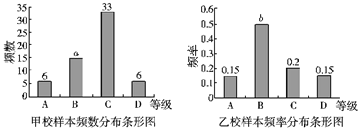
【题目】(文科)(本小题满分12分)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
组号 | 分组 | 频数 | 频率 |
第一组 | [230,235) | 8 | 0.16 |
第二组 | [235,240) | ① | 0.24 |
第三组 | [240,245) | 15 | ② |
第四组 | [245,250) | 10 | 0.20 |
第五组 | [250,255] | 5 | 0.10 |
合 计 | 50 | 1.00 | |
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.