题目内容
【题目】已知![]() .
.
(1)求函数![]() 的定义域;
的定义域;
(2)判断函数![]() 的奇偶性,并予以证明;
的奇偶性,并予以证明;
(3)求使![]() 的
的![]() 的取值范围.
的取值范围.
【答案】(1){x|1<x<1};(2)奇函数;(3)当a>1时,(0,1);当0<a<1时, (1,0).
【解析】
(1)根据对数函数的真数大于0建立关系式可求出函数的定义域;(2)判断函数f(x)-g(x)的奇偶性直接利用函数奇偶性的定义;(3)讨论a与1的大小关系,根据函数的单调性建立关系式,解之即可,需注意函数的定义域.
(1)使函数f(x)g(x)有意义,必须有:1+x>0且1x>0解得:1<x<1
所以函数f(x)g(x)的定义域是{x|1<x<1}
(2)函数f(x)g(x)是奇函数
证明:∵x∈(1,1),x∈(1,1),
f(x)g(x)=loga(1x)loga(1+x)
=[loga(1+x)loga(1x)]=[f(x)g(x)]
∴函数f(x)g(x)是奇函数
(3)使f(x)g(x)>0,即loga(1+x)>loga(1x)
当a>1时,有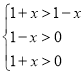 解得x的取值范围是(0,1);
解得x的取值范围是(0,1);
当0<a<1时,有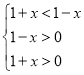 解得x的取值范围是(1,0)
解得x的取值范围是(1,0)

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案【题目】随着节能减排意识深入人心,共享单车在各大城市大范围推广,越来越多的市民在出行时喜欢选择骑行共享单车.为了研究广大市民在共享单车上的使用情况,某公司在我市随机抽取了100名用户进行调查,得到如下数据:
每周使用次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)如果用户每周使用共享单车超过3次,那么认为其“喜欢骑行共享单车”.请完成下面的2×2列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关;
不喜欢骑行共享单车 | 喜欢骑行共享单车 | 合计 | |
男 | |||
女 | |||
合计 |
(2)每周骑行共享单车6次及6次以上的用户称为“骑行达人”,将频率视为概率,在我市所有的“骑行达人”中随机抽取4名,求抽取的这4名“骑车达人”中,既有男性又有女性的概率.
附表及公式: ,其中
,其中![]() ;
;
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |