题目内容
在平面直角坐标系 中,已知过点
中,已知过点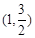 的椭圆
的椭圆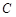 :
: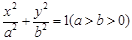 的右焦点为
的右焦点为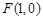 ,过焦点
,过焦点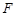 且与
且与 轴不重合的直线与椭圆
轴不重合的直线与椭圆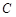 交于
交于 ,
, 两点,点
两点,点 关于坐标原点的对称点为
关于坐标原点的对称点为 ,直线
,直线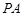 ,
,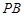 分别交椭圆
分别交椭圆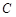 的右准线
的右准线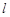 于
于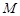 ,
,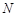 两点.
两点.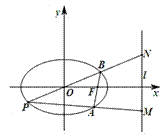
(1)求椭圆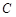 的标准方程;
的标准方程;
(2)若点 的坐标为
的坐标为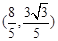 ,试求直线
,试求直线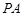 的方程;
的方程;
(3)记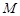 ,
,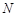 两点的纵坐标分别为
两点的纵坐标分别为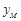 ,
,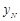 ,试问
,试问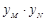 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
(1)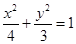 ,(2)
,(2) ,(3)
,(3)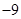 .
.
解析试题分析:(1)求椭圆方程,基本方法是待定系数法.关键是找全所需条件. 椭圆中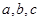 三个未知数的确定只需两个独立条件,根据椭圆定义:点
三个未知数的确定只需两个独立条件,根据椭圆定义:点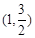 到两个焦点距离和为
到两个焦点距离和为 ,求出
,求出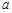 的值,再由
的值,再由 求出
求出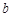 的值,就可得到椭圆的标准方程(2)由点
的值,就可得到椭圆的标准方程(2)由点 关于坐标原点的对称点为
关于坐标原点的对称点为 ,可直接写出点
,可直接写出点 坐标;又由点
坐标;又由点
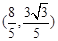 及
及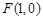 ,可得直线
,可得直线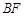 方程,再由
方程,再由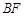 方程与椭圆方程解出A点坐标,根据两点式就可写出直线
方程与椭圆方程解出A点坐标,根据两点式就可写出直线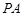 的方程,(3)直线与椭圆位置关系问题就要从其位置关系出发,先根据直线AB垂直
的方程,(3)直线与椭圆位置关系问题就要从其位置关系出发,先根据直线AB垂直 轴的特殊情况下探求
轴的特殊情况下探求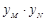 的值,再利用点共线及点在椭圆上条件,逐步消元,直到定值.本题难点在如何利用条件消去参数. 点共线可得到坐标关系,而利用点差法得到斜率关系是解决本题的关键.
的值,再利用点共线及点在椭圆上条件,逐步消元,直到定值.本题难点在如何利用条件消去参数. 点共线可得到坐标关系,而利用点差法得到斜率关系是解决本题的关键.
试题解析:(1)由题意,得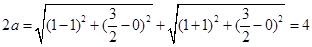 ,即
,即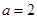 , 2分
, 2分
又 ,
,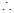
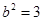 ,
,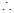 椭圆
椭圆 的标准方程为
的标准方程为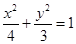 . 5分
. 5分
(2)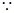
 ,
,
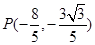 ,又
,又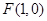 ,
, 
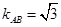 ,
,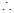 直线
直线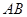 :
: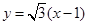 , 7分
, 7分
联立方程组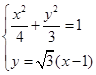 ,解得
,解得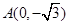 , 9分
, 9分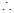 直线
直线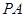 :
: ,即
,即 . 10分
. 10分
(3)当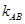 不存在时,易得
不存在时,易得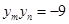 ,
,
当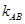 存在时,设
存在时,设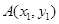 ,
,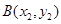 ,则
,则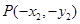 ,
,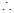
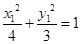 ,
,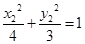 ,两式相减, 得
,两式相减, 得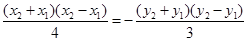 ,
,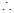
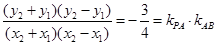 ,令
,令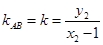 ,则
,则 , 12分
, 12分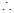 直线
直线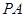 方程:
方程: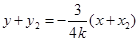 ,
,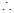
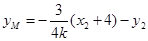 ,
,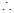
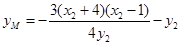 ,
, 直线
直线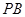 方程:
方程: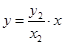 ,
,
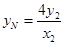 , 14分
, 14分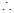
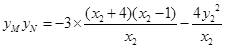 ,又
,又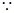
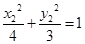 ,
,
练习册系列答案
相关题目
 ,左、右两个焦点分别为
,左、右两个焦点分别为 、
、 ,上顶点
,上顶点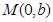 ,
, 为正三角形且周长为6,直线
为正三角形且周长为6,直线 与椭圆
与椭圆 相交于
相交于 两点.
两点. 的取值范围.
的取值范围.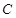 :
: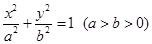 的左、右焦点分别为
的左、右焦点分别为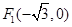 、
、 ,椭圆上的点
,椭圆上的点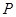 满足
满足 ,且△
,且△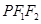 的面积为
的面积为 .
.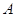 、
、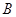 ,过点
,过点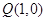 的动直线
的动直线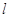 与椭圆
与椭圆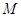 、
、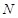 两点,直线
两点,直线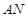 与直线
与直线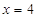 的交点为
的交点为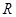 ,证明:点
,证明:点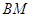 上.
上.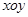 中,已知
中,已知 分别是椭圆
分别是椭圆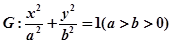 的左、右焦点,椭圆
的左、右焦点,椭圆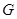 与抛物线
与抛物线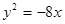 有一个公共的焦点,且过点
有一个公共的焦点,且过点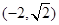 .
.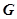 的方程;
的方程;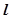 与椭圆
与椭圆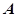 、
、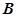 两点,若
两点,若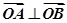 (
(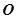 为坐标原点),试判断直线
为坐标原点),试判断直线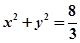 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.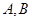 是抛物线
是抛物线 上的两个点,点
上的两个点,点 的坐标为
的坐标为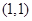 ,直线
,直线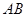 的斜率为
的斜率为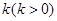 .设抛物线
.设抛物线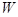 的焦点在直线
的焦点在直线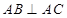 ,过
,过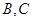 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为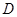 . 判断四边形
. 判断四边形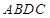 是否为梯形,并说明理由.
是否为梯形,并说明理由.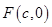 是椭圆
是椭圆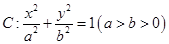 的右焦点;圆
的右焦点;圆 与
与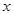 轴交于
轴交于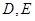 两点,其中
两点,其中 是椭圆
是椭圆 的左焦点.
的左焦点.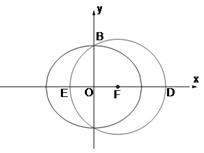
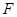 与
与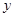 轴的正半轴的交点为
轴的正半轴的交点为 ,点
,点 是点
是点 关于
关于 与圆
与圆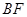 与圆
与圆 ,若
,若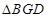 的面积为
的面积为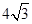 ,求椭圆
,求椭圆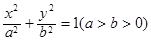 的离心率为
的离心率为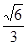 ,长轴长为
,长轴长为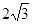 .
.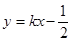 交椭圆C于A、B两点,试问:在y轴正半轴上是否存在一个定点M满足
交椭圆C于A、B两点,试问:在y轴正半轴上是否存在一个定点M满足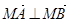 ,若存在,求出点M的坐标;若不存在,请说明理由.
,若存在,求出点M的坐标;若不存在,请说明理由.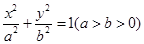 ,若椭圆C的一个焦点为F(
,若椭圆C的一个焦点为F(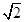 ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为 .
.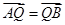 且
且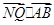 =0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围.
=0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围.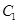 的方程为
的方程为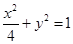 ,双曲线
,双曲线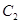 的左、右焦点分别为
的左、右焦点分别为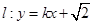 与椭圆
与椭圆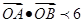 (其中O为原点),求
(其中O为原点),求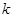 的取值范围。
的取值范围。