题目内容
【题目】某大学高等数学这学期分别用![]() 两种不同的数学方式试验甲、乙两个大一新班(人数均为
两种不同的数学方式试验甲、乙两个大一新班(人数均为![]() 人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各
人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各![]() 名的高等数学期末考试成绩,得到茎叶图:
名的高等数学期末考试成绩,得到茎叶图:
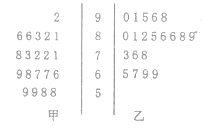
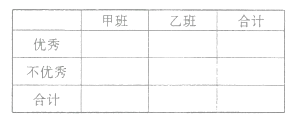
(1)学校规定:成绩不得低于85分的为优秀,请填写下面的![]() 列联表,并判断“能否在犯错误率的概率不超过0.025的前提下认为成绩优异与教学方式有关?”
列联表,并判断“能否在犯错误率的概率不超过0.025的前提下认为成绩优异与教学方式有关?”
下面临界值表仅供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考方式:![]() ,其中
,其中![]() )
)
(2)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题根据茎叶图所提供的数据,填写![]() 列联表,根据独立性检验方法先计算随机变量观测值
列联表,根据独立性检验方法先计算随机变量观测值![]() ,计算要准确,保留3位小数,根据临界值表发现
,计算要准确,保留3位小数,根据临界值表发现![]() ,因此在犯错误的概率不超过0.025的前提下,可以认为成绩优秀与数学方式有关;甲班不低于80分有6人,随机抽取两人,用列举法列出15种情况,至少有1名86分的情况有9种,求出概率值.
,因此在犯错误的概率不超过0.025的前提下,可以认为成绩优秀与数学方式有关;甲班不低于80分有6人,随机抽取两人,用列举法列出15种情况,至少有1名86分的情况有9种,求出概率值.
试题解析:(1)
甲班 | 乙班 | 合计 | |
优秀 |
|
|
|
不优秀 |
|
|
|
合计 |
|
|
|
![]() ,因此在犯错误的概率不超过0.025的前提下,可以认为成绩优秀与数学方式有关.
,因此在犯错误的概率不超过0.025的前提下,可以认为成绩优秀与数学方式有关.
(2)甲班不低于80分有6人,随机抽取两人,用列举法列出15种情况,至少有1名86分的情况有9种,![]()

【题目】某脐橙种植基地记录了10棵脐橙树在未使用新技术的年产量(单位:![]() )和使用了新技术后的年产量的数据变化,得到表格如下:
)和使用了新技术后的年产量的数据变化,得到表格如下:
未使用新技术的10棵脐橙树的年产量
第一棵 | 第二棵 | 第三棵 | 第四棵 | 第五棵 | 第六棵 | 第七棵 | 第八棵 | 第九棵 | 第十棵 | |
年产量 | 30 | 32 | 30 | 40 | 40 | 35 | 36 | 45 | 42 | 30 |
使用了新技术后的10棵脐橙树的年产量
第一棵 | 第二棵 | 第三棵 | 第四棵 | 第五棵 | 第六棵 | 第七棵 | 第八棵 | 第九棵 | 第十棵 | |
年产量 | 40 | 40 | 35 | 50 | 55 | 45 | 42 | 50 | 51 | 42 |
已知该基地共有20亩地,每亩地有50棵脐橙树.
(1)估计该基地使用了新技术后,平均1棵脐橙树的产量;
(2)估计该基地使用了新技术后,脐橙年总产量比未使用新技术将增产多少?
(3)由于受市场影响,导致使用新技术后脐橙的售价由原来(未使用新技术时)的每千克10元降为每千克9元,试估计该基地使用新技术后脐橙年总收入比原来增加的百分数.