题目内容
对n∈N*,不等式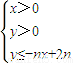 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成一列点:(x1,y1),(x2,y2),(x3,y4),…,(xn,yn)
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成一列点:(x1,y1),(x2,y2),(x3,y4),…,(xn,yn)(1)求xn,yn
(2)若
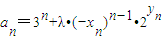 (λ为非零常数),问是否存在整数λ,使得对任意n∈N*,都有an+1>an.
(λ为非零常数),问是否存在整数λ,使得对任意n∈N*,都有an+1>an.
【答案】分析:(1))由-nx+2n>0得x=1,从而得知Dn内的整点都落在直线x=1上且y≤n,因此Dn内的整点按其到原点的距离从近到远排成的点列为:(1,1),(1,2),(1,3),…,(1,n),从而得xn=1,yn=n;
(2)由(1)知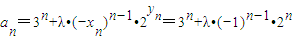 ,先求出an+1-an的表达式,然后分n为奇数和偶数来讨论,当n为奇数时,得λ<1,当n为偶数时,得
,先求出an+1-an的表达式,然后分n为奇数和偶数来讨论,当n为奇数时,得λ<1,当n为偶数时,得 ,又λ≠0且λ∈Z.得知λ=1符合题意.
,又λ≠0且λ∈Z.得知λ=1符合题意.
解答:解:(1)-nx+2n>0⇒x<2,又x>0且x∈N*,∴x=1(1分)
故Dn内的整点都落在直线x=1上且y≤n,故Dn内的整点按其到原点的距离从近到远排成的点列为:(1,1),(1,2),(1,3),…,(1,n),
∴xn=1,yn=n(5分)
(2)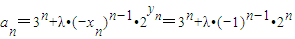 ,
,
∴an+1-an=3n+1+λ•(-1)n•2n+1-[3n+λ•(-1)n-1•2n]=2•3n-3λ•(-1)n-1•2n>0
∴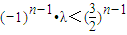 …(*) (8分)
…(*) (8分)
当n=2k-1(k=1,2,3,…)时,(*)式即为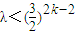 对k=1,2,3,…都成立,∴λ<1(10分)
对k=1,2,3,…都成立,∴λ<1(10分)
当n=2k(k=1,2,3,…)时,(*)式即为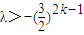 对k=1,2,3,…都成立,∴
对k=1,2,3,…都成立,∴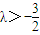 (12分)
(12分)
∴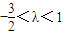 ,又λ≠0且λ∈Z,
,又λ≠0且λ∈Z,
∴存在λ=-1,使得对任意n∈N*,都有an+1>an. (14分)
点评:此题考查简单的平面区域知识,及函数的分类讨论思想.
(2)由(1)知
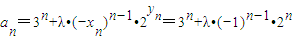 ,先求出an+1-an的表达式,然后分n为奇数和偶数来讨论,当n为奇数时,得λ<1,当n为偶数时,得
,先求出an+1-an的表达式,然后分n为奇数和偶数来讨论,当n为奇数时,得λ<1,当n为偶数时,得 ,又λ≠0且λ∈Z.得知λ=1符合题意.
,又λ≠0且λ∈Z.得知λ=1符合题意.解答:解:(1)-nx+2n>0⇒x<2,又x>0且x∈N*,∴x=1(1分)
故Dn内的整点都落在直线x=1上且y≤n,故Dn内的整点按其到原点的距离从近到远排成的点列为:(1,1),(1,2),(1,3),…,(1,n),
∴xn=1,yn=n(5分)
(2)
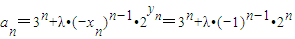 ,
,∴an+1-an=3n+1+λ•(-1)n•2n+1-[3n+λ•(-1)n-1•2n]=2•3n-3λ•(-1)n-1•2n>0
∴
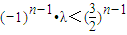 …(*) (8分)
…(*) (8分)当n=2k-1(k=1,2,3,…)时,(*)式即为
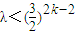 对k=1,2,3,…都成立,∴λ<1(10分)
对k=1,2,3,…都成立,∴λ<1(10分)当n=2k(k=1,2,3,…)时,(*)式即为
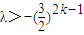 对k=1,2,3,…都成立,∴
对k=1,2,3,…都成立,∴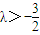 (12分)
(12分)∴
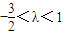 ,又λ≠0且λ∈Z,
,又λ≠0且λ∈Z,∴存在λ=-1,使得对任意n∈N*,都有an+1>an. (14分)
点评:此题考查简单的平面区域知识,及函数的分类讨论思想.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
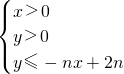 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).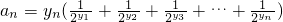 ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;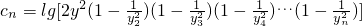 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.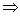 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y4),…,(xn,yn)
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y4),…,(xn,yn)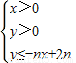 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn). ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;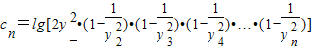 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.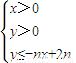 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).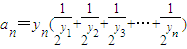 ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;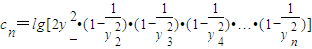 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.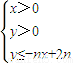 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn). ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn; ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.