题目内容
已知函数 .对于任意实数x恒有
.对于任意实数x恒有
(1)求实数 的最大值;
的最大值;
(2)当 最大时,函数
最大时,函数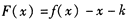 有三个零点,求实数k的取值范围。
有三个零点,求实数k的取值范围。
(1)3;(2)
解析试题分析:(1)根据函数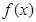 求出导函数,再根据所给的不等式,利用恒成立的条件求出实数
求出导函数,再根据所给的不等式,利用恒成立的条件求出实数 的范围,从而确定
的范围,从而确定 的最大值.
的最大值.
(2)由(1)可得 的值,从而根据函数
的值,从而根据函数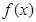 确定函数
确定函数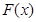 的解析式,由于函数
的解析式,由于函数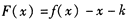 有三个零点,所以通过对函数
有三个零点,所以通过对函数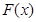 求导,了解函数
求导,了解函数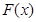 的图像的走向,以及对函数的极值的正负性作出规定,即可得到所需的结论.
的图像的走向,以及对函数的极值的正负性作出规定,即可得到所需的结论.
试题解析:(1)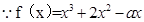
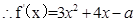 对于
对于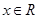 恒有
恒有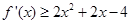 ,即
,即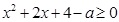 对于
对于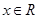 恒成立
恒成立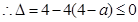
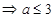
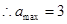
(2)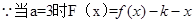 有三个零点
有三个零点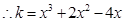 有三个不同的实根
有三个不同的实根 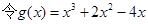 ,则
,则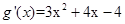
令 解得
解得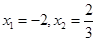
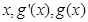 情况如下表:
情况如下表: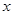
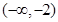
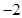
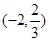
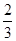
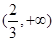
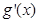
+ 0 - 0 + 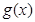
单调递增 极大值8 单调递减 极小极 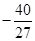
单调递增  练习册系列答案
练习册系列答案

西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
相关题目
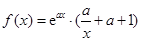 ,其中
,其中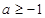 .
.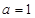 时,求曲线
时,求曲线 在点
在点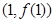 处的切线方程;
处的切线方程; .
. 的极值;
的极值; 在区间
在区间 上的取值范围为
上的取值范围为 ,则称区间
,则称区间 上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由. -1.
-1. x3+
x3+ ,
, .
. 在
在 上的最大值;
上的最大值; 为曲线
为曲线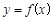 的切线,求实数
的切线,求实数 的值;
的值; 时,设
时,设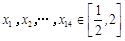 ,且
,且 ,若不等式
,若不等式 恒成立,求实数
恒成立,求实数 的最小值.
的最小值. x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围; +
+ +…+
+…+ >ln(n+1)都成立.
>ln(n+1)都成立.