题目内容
已知函数 .
.
(1)求 在
在 上的最大值;
上的最大值;
(2)若直线 为曲线
为曲线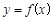 的切线,求实数
的切线,求实数 的值;
的值;
(3)当 时,设
时,设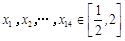 ,且
,且 ,若不等式
,若不等式 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
(1)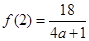 (2)
(2)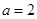 或
或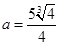 . (3)
. (3) 的最小值为
的最小值为 .
.
解析试题分析:
(1)利用导数可以求解函数单调性得到极值与最值,但是函数含有参数,故而需要讨论,首先对函数求定义域,求导可以发现导函数的分母恒大于0不影响导函数符号,故考虑分子大于0,小于0的解集,讨论a的范围得到区间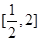 的单调性,分析就可以得到原函数在固定区间上的最值.
的单调性,分析就可以得到原函数在固定区间上的最值.
(2)设出切点坐标,利用切点满足的三个条件(①切点在原函数上,坐标满足原函数方程 ②切点在切线上,坐标满足切线方程 ③原函数在切点处的导数为切线的斜率)建立关于a的方程,解方程求出a的值.
(3)由(2)的结论得到此时直线 为曲线
为曲线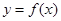 的切线,且分析原函数与切线的图像可以发现曲线
的切线,且分析原函数与切线的图像可以发现曲线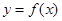 在直线
在直线 下方,即可以发现在区间
下方,即可以发现在区间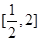 上不等式
上不等式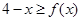 恒成立,作差即可严格证明该不等式是成立的.利用该不等式对
恒成立,作差即可严格证明该不等式是成立的.利用该不等式对 放缩为可求和的式子,进而求的
放缩为可求和的式子,进而求的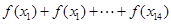 的最值,得到
的最值,得到 的取值范围与最值.
的取值范围与最值.
试题解析:
(1)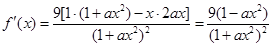 , 2分
, 2分
令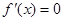 ,解得
,解得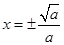 (负值舍去),
(负值舍去),
由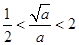 ,解得
,解得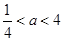 .
.
(ⅰ)当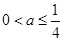 时,由
时,由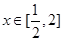 ,得
,得 ,
,
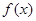 在
在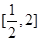 上的最大值为
上的最大值为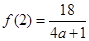 . 3分
. 3分
(ⅱ)当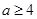 时,由
时,由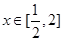 ,得
,得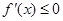 ,
,
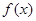 在
在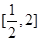 上的最大值为
上的最大值为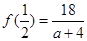 . 4分
. 4分
(ⅲ)当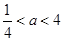 时,
时, 在
在 时,
时,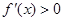 ,在
,在 时,
时, ,
,
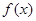 在
在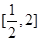 上的最大值为
上的最大值为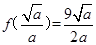 . 5分
. 5分
(2)设切点为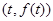 ,则
,则 6分
6分
由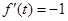 ,有
,有 ,化简得
,化简得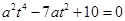 ,
,
即 或
或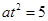 , ①
, ①
由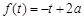 ,有
,有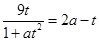 ,②
,②
由①、②解得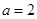 或
或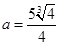 . 9分
. 9分
(3)当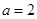 时,
时,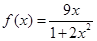 ,
,
由(2)的结论直线 为曲线
为曲线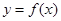 的切线,
的切线,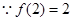 ,
, 点
点 在直线
在直线 上,
上,
根据图像分析,曲线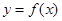 在直线
在直线 下方. 10分
下方. 10分
下面给出证明:当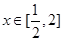 时,
时,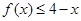 .
.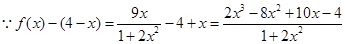

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目

 .对于任意实数x恒有
.对于任意实数x恒有
 的最大值;
的最大值;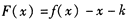 有三个零点,求实数k的取值范围。
有三个零点,求实数k的取值范围。 x3+
x3+ x2+2ax.
x2+2ax. ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围. ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值. (其中
(其中 是自然对数的底)
是自然对数的底) 在
在 处取得极值,求
处取得极值,求 的值;
的值; x2-
x2- 的取值范围.
的取值范围. ;
; ,求
,求 上恒成立,求a的取值范围.
上恒成立,求a的取值范围. ,
, ,
, 图象与
图象与 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为 ,
, 与
与 , 并且
, 并且 的值;
的值; 的取值范围及函数
的取值范围及函数 的最小值;
的最小值; ,给定
,给定 ,对于两个大于1的正数
,对于两个大于1的正数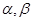 ,存在实数
,存在实数 满足:
满足: ,
, ,并且使得不等式
,并且使得不等式 恒成立,求实数
恒成立,求实数 +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.