题目内容
在空间直角坐标系中,定义:平面α的一般方程为:Ax+By+Cz+D=0(A,B,C,D∈R,且A,B,C不同时为零),点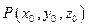 到平面α的距离为:
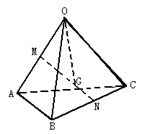
到平面α的距离为: ,则在底面边长与高都为2的正四棱锥中,底面中心O到侧面的距离等于( )
,则在底面边长与高都为2的正四棱锥中,底面中心O到侧面的距离等于( )
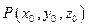 到平面α的距离为:
到平面α的距离为: ,则在底面边长与高都为2的正四棱锥中,底面中心O到侧面的距离等于( )
,则在底面边长与高都为2的正四棱锥中,底面中心O到侧面的距离等于( )A. | B. | C.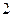 | D.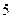 |
B
以底面中心O为原点建立空间直角坐标系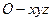 ,则A(1,1,0),B(-1,1,0),P(0,0,2),设平面PAB的方程为Ax+By+Cz+D=0,将以上3个坐标代入计算得A=0,B=-D,
,则A(1,1,0),B(-1,1,0),P(0,0,2),设平面PAB的方程为Ax+By+Cz+D=0,将以上3个坐标代入计算得A=0,B=-D, ,所以-Dy-
,所以-Dy-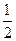 Dz+D=0,即2y+z-2=0,
Dz+D=0,即2y+z-2=0,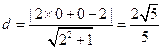 .
.
故选B.
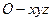 ,则A(1,1,0),B(-1,1,0),P(0,0,2),设平面PAB的方程为Ax+By+Cz+D=0,将以上3个坐标代入计算得A=0,B=-D,
,则A(1,1,0),B(-1,1,0),P(0,0,2),设平面PAB的方程为Ax+By+Cz+D=0,将以上3个坐标代入计算得A=0,B=-D, ,所以-Dy-
,所以-Dy-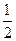 Dz+D=0,即2y+z-2=0,
Dz+D=0,即2y+z-2=0,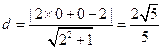 .
.故选B.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
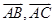 为边的平行四边形的面积为________.
为边的平行四边形的面积为________.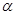 、
、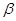 的法向量分别为
的法向量分别为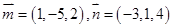 ,则 ( )
,则 ( )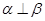
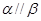
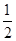 ,y=-
,y=-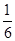 ,y=-
,y=-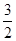
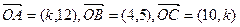 ,且A、B、C三点共线,则
,且A、B、C三点共线,则
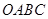 ,其对角线为
,其对角线为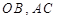 ,
,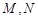 分别是边
分别是边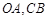 的中点,点
的中点,点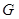 在线段
在线段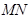 上,且使
上,且使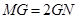 ,用向量
,用向量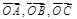 表示向量
表示向量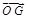 是 ( )
是 ( )