题目内容
已知在棱长为2的正方体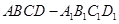 中,
中,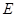 为
为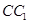 的中点.
的中点.
(1)求证: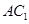 ∥
∥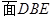 ;
;
(2)求三棱锥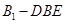 的体积.
的体积.
(1)详见解析;(2)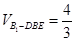 .
.
解析试题分析:(1)要证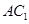 ∥面
∥面 ,只须在平面
,只须在平面 内找到一条直线与
内找到一条直线与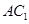 平行,这条直线就是过直线
平行,这条直线就是过直线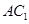 的一个平面
的一个平面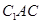 与平面
与平面 的交线
的交线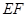 (其中
(其中 ),然后根据三角形中位线的性质可证得交线
),然后根据三角形中位线的性质可证得交线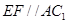 ,最后由线面平行的判定进行证明即可;(2)由
,最后由线面平行的判定进行证明即可;(2)由 可知,要求三棱锥
可知,要求三棱锥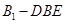 的体积,只须求三棱锥
的体积,只须求三棱锥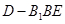 的体积,该三棱锥的高就是
的体积,该三棱锥的高就是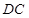 ,根据三棱锥的体积计算公式即可求出三棱锥
,根据三棱锥的体积计算公式即可求出三棱锥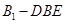 的体积.
的体积.
试题解析:(1)证明:如图,连接 交
交 于点
于点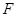 ,连接
,连接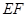

则由题在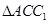 中,
中,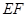 是两边
是两边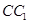 、
、 上的中位线
上的中位线
∴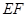 ∥
∥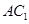 4分
4分
又∵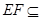 面
面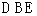
∴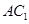 ∥面
∥面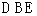 6分
6分
(2)解:由题 8分
8分
而在三棱锥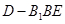 中,
中,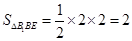 ,高为正方体的棱长
,高为正方体的棱长
∴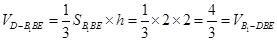 ,即
,即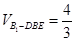 12分.
12分.
考点:1.空间几何体的体积计算;2.线面平行的证明.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
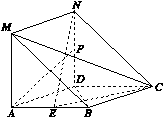
 为直角梯形,
为直角梯形,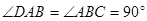 ,
,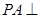 平面
平面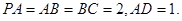
 平面
平面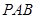 ;
; 所成锐二面角的余弦值.
所成锐二面角的余弦值.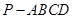 中,底面
中,底面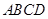 是边长为2的正方形,侧面
是边长为2的正方形,侧面 底面
底面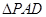 为等腰直角三角形,
为等腰直角三角形, ,
,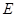 、
、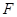 分别为
分别为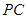 、
、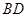 的中点.
的中点.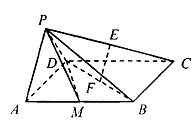
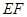 //平面
//平面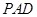 ;
;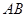 中点为
中点为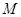 ,求二面角
,求二面角 的余弦值.
的余弦值. 与
与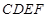 均为正方形,平面
均为正方形,平面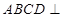 平面
平面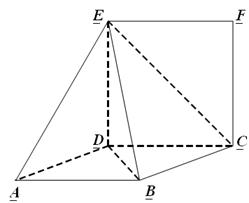
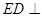 平面
平面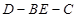 的大小.
的大小.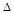 ACD沿AC折起至
ACD沿AC折起至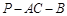 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.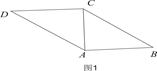
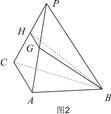
 平面BGH;
平面BGH;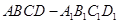 中,E为
中,E为 的中点.
的中点.
 ;
;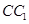 所成的角的正弦值.
所成的角的正弦值.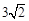 ,点M,N分别在PA,BD上,且
,点M,N分别在PA,BD上,且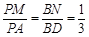 .
.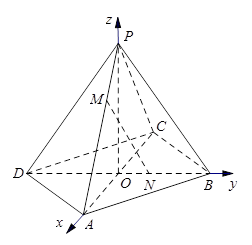

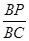 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.