题目内容
如图,已知四边形 与
与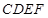 均为正方形,平面
均为正方形,平面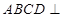 平面
平面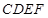 .
.
(1)求证: 平面
平面 ;
;
(2)求二面角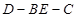 的大小.
的大小.
(1)详见解析;(2)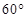 .
.
解析试题分析:(1)要证直线与平面垂直,只须证明这条直线与平面内的两条相交直线垂直或证明这条直线是两垂直平面中一个平面内的一条直线,且这条直线垂直于这两个平面的交线即可.本题属于后者,由平面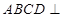 平面
平面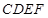 且交线为
且交线为 ,而
,而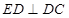 且
且 平面
平面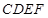 ,所以问题得证;(2)解决空间角最有效的工具是向量法,先以点
,所以问题得证;(2)解决空间角最有效的工具是向量法,先以点 为坐标原点,利用已有的垂直关系建立空间直角坐标系,为计算的方便,不妨设正方形的边长为1,然后标出有效点与有效向量的坐标,易知平面
为坐标原点,利用已有的垂直关系建立空间直角坐标系,为计算的方便,不妨设正方形的边长为1,然后标出有效点与有效向量的坐标,易知平面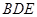 的法向量为
的法向量为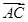 ,再利用待定系数法求出另一平面
,再利用待定系数法求出另一平面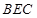 的法向量,接着计算出这两个法向量夹角的余弦值,根据二面角的图形与计算出的余弦值,确定二面角的大小即可.
的法向量,接着计算出这两个法向量夹角的余弦值,根据二面角的图形与计算出的余弦值,确定二面角的大小即可.
试题解析:(1)因为平面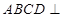 平面
平面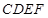 ,且平面
,且平面
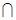 平面
平面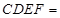

又因为四边形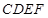 为正方形,所以
为正方形,所以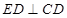
因为 平面
平面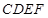 ,所以
,所以 平面
平面 4分
4分
(2)以 为坐标原点,如图建立空间直角坐标系
为坐标原点,如图建立空间直角坐标系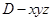
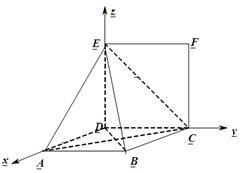
则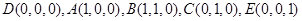
所以平面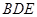 的法向量为
的法向量为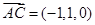 5分
5分
设平面 的法向量为
的法向量为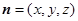
因为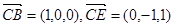
由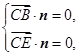 得
得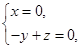 即
即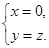
令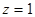 ,则
,则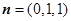 6分
6分
因为
所以二面角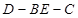 的大小为
的大小为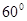 8分.
8分.
考点:1.面面垂直的性质;2.线面垂直的证明;3.空间角的计算.

练习册系列答案
相关题目
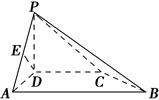
 平面
平面 ,
,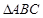 是等腰直角三角形,
是等腰直角三角形, ,四边形
,四边形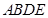 是直角梯形,
是直角梯形, ∥AE,
∥AE,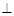
 ,
,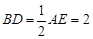 ,
, 分别为
分别为 的中点.
的中点.
 与
与 所成角的大小;
所成角的大小;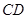 和平面
和平面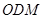 所成角的正弦值.
所成角的正弦值. 平面
平面 ,四边形
,四边形 为矩形,
为矩形,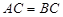 .
.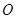 为
为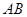 的中点,
的中点, .
.
 ;
; 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的余弦值.
的余弦值. ,
,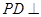 面
面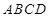 ,
,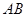 ∥
∥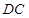 ,
,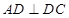 ,
,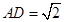 ,
,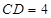 ,
,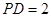 ,
,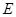 为
为 上一点,
上一点,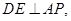
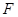 是平面
是平面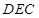 与
与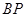 的交点.
的交点.
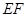 ∥
∥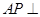 面
面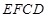 ;
; 与面
与面 中,
中, 为
为 的中点.
的中点. ∥
∥ ;
; 的体积.
的体积.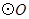 的直径
的直径 ,点
,点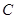 、
、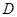 为
为 ,
,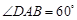 ,
,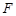 为弧
为弧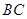 的中点.将
的中点.将 折起,使两个半圆所在平面互相垂直(如图2).
折起,使两个半圆所在平面互相垂直(如图2).
 ;
;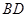 上是否存在点
上是否存在点 ,使得
,使得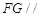 平面
平面 ?若存在,试指出点
?若存在,试指出点 的正弦值.
的正弦值.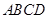 中,
中,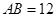 ,
,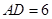 ,
,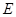 、
、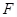 分别为
分别为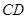 、
、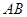 边上的点,且
边上的点,且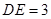 ,
,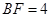 ,将
,将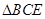 沿
沿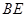 折起至
折起至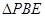 位置(如图2所示),连结
位置(如图2所示),连结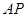 、
、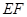 、
、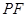 ,其中
,其中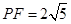 .
.
 平面
平面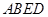 ;
;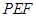 所成角的正弦值.
所成角的正弦值.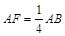 .
.