题目内容
【题目】在![]() 中,
中,![]() 为直角,
为直角,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.
(1)试用![]() 、
、![]() 表示向量
表示向量![]() ;
;
(2)在线段![]() 上取一点
上取一点![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,使得直线
,使得直线![]() 过
过![]() ,设
,设![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,过
,过![]() 作线段
作线段![]() ,使得
,使得![]() 为
为![]() 的中点,且
的中点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设![]() ,根据
,根据![]() ,
,![]() ,
,![]() 三点共线,可得存在非零实数
三点共线,可得存在非零实数![]() 使得
使得![]() ,从而
,从而![]() ,,利用平面向量基本定理可得
,,利用平面向量基本定理可得![]() ,
,![]() 的关系,同理
的关系,同理![]() ,
,![]() ,
,![]() 三点共线,可得
三点共线,可得![]() ,
,![]() 的关系,由此即可求得
的关系,由此即可求得![]() ,
,![]() 的值,即得解;(2)将
的值,即得解;(2)将![]() 两次线性表示,利用平面向量基本定理,建立等式,消参,即可证得结论
两次线性表示,利用平面向量基本定理,建立等式,消参,即可证得结论
(3)如图,设![]() 的夹角为
的夹角为![]() ,则
,则![]() 的夹角为
的夹角为![]() ,求出
,求出![]() ,再求取值范围.
,再求取值范围.
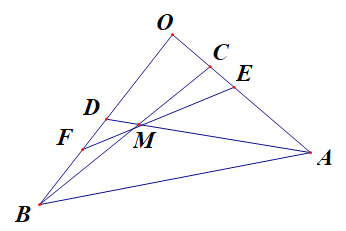
(1)解:设![]()
![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() 存在非零实数
存在非零实数![]() 使得
使得![]()
![]()
![]() ,
,
![]()
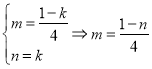 ①
①
又![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() 存在非零实数
存在非零实数![]() 使得
使得![]()
![]()
![]() ,
,
又![]()
![]()
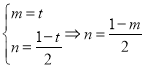 ②
②
由①②解得:![]() ,
,
所以![]() .
.
(2)证明:由(1)知![]() ,
,
![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
![]() 存在非零实数
存在非零实数![]() 使得
使得![]()
![]()
![]()
![]()
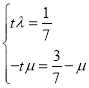
消去![]() 得
得![]() .
.
所以![]() .
.
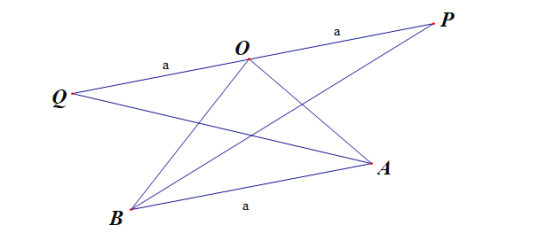
(3)
如图,设![]() 的夹角为
的夹角为![]() ,则
,则![]() 的夹角为
的夹角为![]() ,
,
![]()
所以![]()
所以![]()
所以![]() .
.

练习册系列答案
相关题目
