题目内容
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在定义域上是增函数,求实数
在定义域上是增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,令
,令![]() ,试讨论函数
,试讨论函数![]() 的零点个数,并说明理由.
的零点个数,并说明理由.
【答案】(Ⅰ)![]() .(Ⅱ)见解析
.(Ⅱ)见解析
【解析】试题分析:(1)函数在某区间上为增函数就是要求函数的导数在某区间上非负,求出函数的导数,由于含参,所以对参数分类两种情况讨论,当![]() 时,导数非负恒成立,当
时,导数非负恒成立,当![]() ,导数值有正有负有零,不合题意舍;(2)写出函数F(x)并求导,分m=1和m>1两种情况研究,当m=1时,函数单调减,一个零点,当 m>1时,写出函数的单调区间,图象先减后增再减,由于极小值为正,只能当极大值小于零时,才会有一个零点,解出m的范围 .
,导数值有正有负有零,不合题意舍;(2)写出函数F(x)并求导,分m=1和m>1两种情况研究,当m=1时,函数单调减,一个零点,当 m>1时,写出函数的单调区间,图象先减后增再减,由于极小值为正,只能当极大值小于零时,才会有一个零点,解出m的范围 .
试题解析:
(Ⅰ)依题意得, ![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,故函数
,故函数![]() 在
在![]() 上单调递增,符合题意;
上单调递增,符合题意;
当![]() 时,
时, 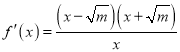 ,
,
令![]() ,得
,得![]() ,函数
,函数![]() 单调递减,
单调递减,
令![]() ,得
,得![]() ,函数
,函数![]() 单调递增,
单调递增,
故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,不合题意.
上单调递增,不合题意.
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ)![]() (
(![]() ),
),
易得![]() .
.
①若![]() ,则
,则![]() ,函数
,函数![]() 为减函数,
为减函数,
注意到![]() ,
, ![]() ,所以
,所以![]() 有唯一零点;
有唯一零点;
②若![]() ,则当
,则当![]() 或
或![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以函数![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
注意到![]() ,
, ![]() ,所以
,所以![]() 有唯一零点.
有唯一零点.
综上,当![]() 时,函数
时,函数![]() 有唯一零点.
有唯一零点.

 通城学典默写能手系列答案
通城学典默写能手系列答案【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
(A)2号学生进入30秒跳绳决赛
(B)5号学生进入30秒跳绳决赛
(C)8号学生进入30秒跳绳决赛
(D)9号学生进入30秒跳绳决赛
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程![]() =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程![]() =
=![]() x+
x+![]() 必过(
必过(![]() ,
,![]() );
);
④在一个2×2列联表中,由计算得K2=13.079,则有99%以上的把握认为这两个变量间有关系.
其中错误的个数是( )
本题可以参考独立性检验临界值表:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
A. 0 B. 1
C. 2 D. 3