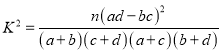题目内容
【题目】设函数![]() .
.
①若![]() 有两个零点,则实数
有两个零点,则实数![]() 的取值范围是 ___________;
的取值范围是 ___________;
②若![]() ,则满足
,则满足![]()
![]() 的
的![]() 的取值范围是 _________________.
的取值范围是 _________________.
【答案】 ![]()
![]()
【解析】①若a=0,则![]() ,
,
由f(x)=0,可得x=0,x=﹣![]() ,符合题意;
,符合题意;
若a<0,x=0符合题意;
若x=﹣![]() 符合题意,则a>﹣
符合题意,则a>﹣![]() ,即为﹣
,即为﹣![]() <a<0;
<a<0;
若a>0,则x=0和x=﹣![]() 符合题意,可得a≤
符合题意,可得a≤![]() ,
,
综上可得,a的范围是(﹣![]() ,
,![]() ];
];
②若x<a≤﹣2,则x﹣1<a﹣1≤﹣3,
f(x)的导数为3x2﹣3>0,
可得f(x)<f(﹣2)=﹣2,f(x﹣1)<﹣27+9=﹣18,
即有f(x)+f(x﹣1)<﹣30,不符题意;
则x≥a,若x﹣1≥a,f(x)+f(x﹣1)>﹣3,
即为x+x﹣1>﹣3,解得x>﹣1;
若a﹣1≤x﹣1<a,f(x)+f(x﹣1)>﹣3,
即为x+(x﹣1)3﹣3(x﹣1)>﹣3,
化为x3﹣3x2+x+5>0,
由于a≤﹣2,且a≤x<a+1,
可得g(x)=x3﹣3x2+x+5的导数g′(x)=3x2﹣6x+1>0,
即g(x)在[a,a+1)递增,g(a)取得最小值,且为a3﹣3a2+a+5,
且a3﹣3a2+a+5,
而在a≤﹣2时,a3﹣3a2+a+5递增,且为负值,不符题意.
综上可得a的范围是(﹣1,+∞).
故填![]() ,(﹣1,+∞).
,(﹣1,+∞).

【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
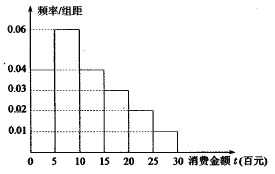
【题目】以“你我中国梦,全民建小康”为主题“社会主义核心价值观”为主线,为了解![]() 、
、![]() 两个地区的观众对2018年韩国平昌冬奥会准备工作的满意程度,对
两个地区的观众对2018年韩国平昌冬奥会准备工作的满意程度,对![]() 、
、![]() 地区的
地区的![]() 名观众进行统计,统计结果如下:
名观众进行统计,统计结果如下:
非常满意 | 满意 | 合计 | |
|
|
| |
|
|
| |
合计 |
在被调查的全体观众中随机抽取![]() 名“非常满意”的人是
名“非常满意”的人是![]() 地区的概率为
地区的概率为![]() ,且
,且![]() .
.
(1)现从![]() 名观众中用分层抽样的方法抽取
名观众中用分层抽样的方法抽取![]() 名进行问卷调查,则应抽取“满意”的
名进行问卷调查,则应抽取“满意”的![]() 、
、![]() 地区的人数各是多少?
地区的人数各是多少?
(2)在(1)抽取的“满意”的观众中,随机选出![]() 人进行座谈,求至少有两名是
人进行座谈,求至少有两名是![]() 地区观众的概率?
地区观众的概率?
(3)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系?
的把握认为观众的满意程度与所在地区有关系?
附:
|
|
|
|
|
|
|
|
,![]()