题目内容
已知:数列{an}的前n项和为Sn,满足Sn=2an-2n(n∈N*)
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=log2(an+2),而Tn为数列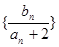 的前n项和,求Tn.
的前n项和,求Tn.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=log2(an+2),而Tn为数列
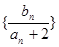 的前n项和,求Tn.
的前n项和,求Tn.(1)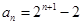 (2)
(2)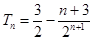
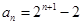 (2)
(2)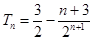
试题分析:(1)当n∈N*时,Sn=2an-2n,①
则当n≥2, n∈N*时,Sn-1=2an-1-2(n-1). ②
①-②,得an=2an-2an-1-2,即an=2an-1+2,
∴an+2=2(an-1+2) ∴
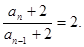
当n="1" 时,S1=2a1-2,则a1=2,当n=2时,a2=6,
∴ {an+2}是以a1+2为首项,以2为公比的等比数列.
∴an+2=4·2n-1,∴an=2n+1-2,………6分
(2)由
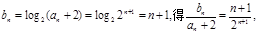
则
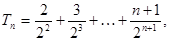 ③
③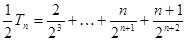 ,④
,④③-④,得
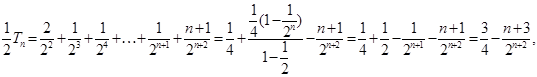
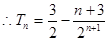 ………………………12分
………………………12分点评:由
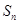 求通项
求通项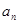 及错位相减求和是数列问题常考知识点
及错位相减求和是数列问题常考知识点
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
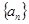 是递增数列,且满足
是递增数列,且满足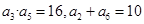 。
。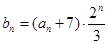 ,求数列
,求数列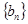 的前
的前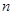 项和
项和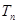 。
。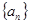 的前
的前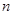 项和为
项和为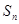 ,已知
,已知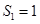 ,
,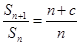 (
(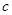 为常数,
为常数,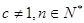 ),且
),且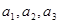 成等差数列.
成等差数列.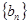 是首项为1,公比为
是首项为1,公比为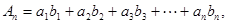
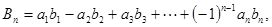
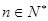
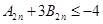 ,(
,(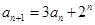 ,(n∈N﹡),且
,(n∈N﹡),且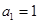 ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .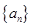 是等差数列,其中
是等差数列,其中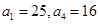 .
.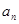 ;
;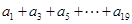 值.
值.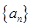 的前
的前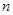 项和为
项和为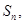
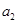 、
、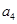 是方程
是方程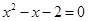 的两个根,则
的两个根,则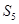 等于( )
等于( )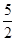
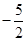
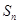 表示等差数列
表示等差数列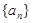 的前
的前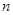 项和,且
项和,且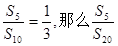 等于( )
等于( )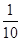
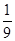
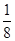
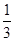
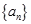 的前n项和为
的前n项和为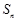 ,且满足
,且满足 ,
, =1,2,3,….
=1,2,3,….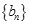 满足
满足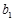 =1,且
=1,且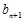 =
=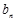 +
+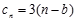 ,求数列
,求数列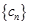 的前
的前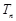 .
.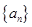 是公差不为零的等差数列,
是公差不为零的等差数列,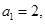 且
且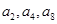 成等比数列
成等比数列 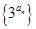 的前
的前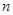 项和
项和