题目内容
设数列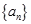 的前n项和为
的前n项和为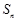 ,且满足
,且满足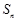 =2-
=2- ,
, =1,2,3,….
=1,2,3,….
(1)求数列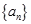 的通项公式;
的通项公式;
(2)若数列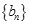 满足
满足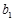 =1,且
=1,且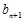 =
=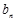 +
+ ,求数列
,求数列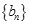 的通项公式;
的通项公式;
(3)设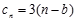 ,求数列
,求数列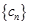 的前
的前 项和为
项和为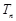 .
.
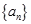 的前n项和为
的前n项和为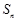 ,且满足
,且满足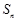 =2-
=2- ,
, =1,2,3,….
=1,2,3,….(1)求数列
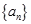 的通项公式;
的通项公式;(2)若数列
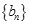 满足
满足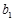 =1,且
=1,且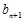 =
=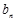 +
+ ,求数列
,求数列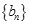 的通项公式;
的通项公式;(3)设
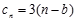 ,求数列
,求数列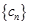 的前
的前 项和为
项和为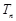 .
.(1) =
=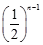 ( n∈
( n∈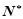 )(2)
)(2)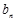 =
=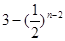 (
( =1,2,3,…)
=1,2,3,…)
(3)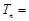 8-
8-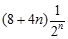
 =
=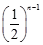 ( n∈
( n∈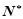 )(2)
)(2)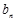 =
=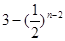 (
( =1,2,3,…)
=1,2,3,…)(3)
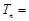 8-
8-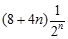
试题分析:(1)因为
 =1时,
=1时,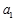 +
+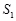 =
=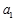 +
+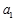 =2,所以
=2,所以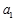 =1.
=1.因为
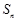 =2-
=2- ,即
,即 +
+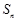 =2,所以
=2,所以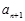 +
+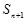 =2.
=2.两式相减:
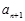 -
- +
+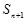 -
-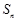 =0,即
=0,即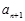 -
- +
+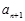 =0,故有
=0,故有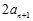 =
= .
.因为
 ≠0,所以
≠0,所以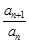 =
=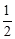 ( n∈
( n∈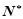 ).
).所以数列
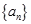 是首项
是首项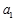 =1,公比为
=1,公比为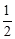 的等比数列,
的等比数列,所以
 =
=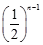 (
(  ∈
∈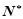 ). ……5分
). ……5分(2)因为
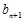 =
=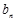 +
+ ( n=1,2,3,…),所以
( n=1,2,3,…),所以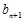 -
-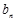 =
=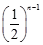 .从而有
.从而有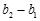 =1,
=1,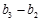 =
=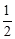 ,
,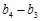 =
=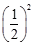 ,…,
,…, =
=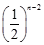 (
(  =2,3,…).
=2,3,…).将这
 -1个等式相加,得
-1个等式相加,得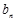 -
-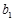 =1+
=1+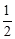 +
+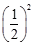 +…+
+…+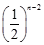 =
=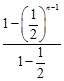 =2-
=2-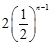 .(
.( =2,3,…).
=2,3,…).又因为
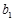 =1,所以
=1,所以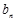 =3-
=3-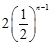 (
(  =2,3,…).
=2,3,…).经检验,对
 =1也成立,
=1也成立,故
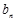 =3-
=3-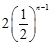 =
=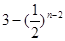 (
( =1,2,3,…). ……10分
=1,2,3,…). ……10分(3)因为
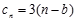 =
=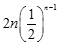 ,
,所以
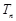 =
=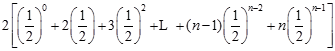 . ①
. ①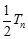 =
=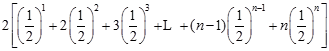 . ②
. ②①-②,得
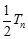 =
=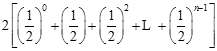 -
-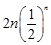 .
. 故
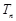 =
=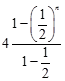 -
-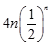 =8-
=8-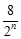 -
-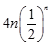 =8-
=8-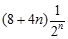 ( n=1,2,3,…).
( n=1,2,3,…).……15分
点评:一般解数列的解答题时会给出一个递推关系式,此时一般情况下会再写一个作差,写的时候要特别注意首项是否能取到,另外错位相减法求和是高考中常考的内容,要多加练习.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
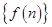 的前n项和为
的前n项和为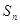 ,且
,且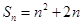 .
.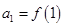 ,
,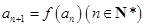 ,求证数列
,求证数列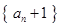 是等比数列,并求数
是等比数列,并求数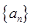 的前
的前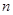 项和
项和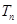 .
. 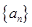 的各项均为正实数,且其前
的各项均为正实数,且其前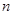 项和
项和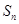 满足
满足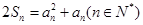 。(1)证明:数列
。(1)证明:数列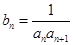 ,求数列
,求数列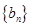 的前
的前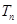 。
。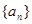 的前
的前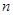 项和为
项和为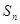 ,若
,若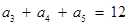 ,则
,则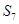 的值为 .
的值为 .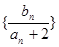 的前n项和,求Tn.
的前n项和,求Tn.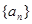 满足
满足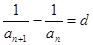 (其中d为常数,
(其中d为常数,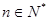 ),则称数列
),则称数列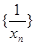 为调和数列,且
为调和数列,且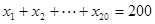 ,则
,则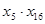 的最大值为 .
的最大值为 .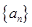 的前项和为
的前项和为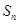 ,若
,若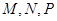 三点共线,
三点共线,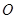 为坐标原点,且
为坐标原点,且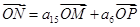 (直线
(直线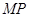 不过点
不过点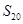 等于 ( )
等于 ( )



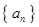 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d,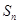 为其前n项和,且满足
为其前n项和,且满足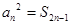 ,
,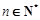 .数列
.数列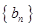 满足
满足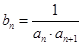 ,
,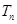 为数列
为数列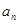 和数列
和数列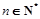 ,不等式
,不等式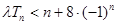 恒成立,求实数
恒成立,求实数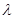 的取值范围;
的取值范围;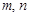
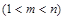 ,使得
,使得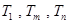 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有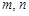 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.