题目内容
(2013•惠州一模)已知椭圆的中心在原点,焦点在x轴上,一个顶点为B(0,-1),且其右焦点到直线x-y+2
=0的距离为3.
(1)求椭圆方程;
(2)设直线l过定点Q(0,
),与椭圆交于两个不同的点M、N,且满足|BM|=|BN|.求直线l的方程.
| 2 |
(1)求椭圆方程;
(2)设直线l过定点Q(0,
| 3 |
| 2 |
分析:(1)设椭圆方程为
+
=1(a>b>0),易知b=1,设右焦点F(c,0),由条件得3=
,可求得c值,根据a2=b2+c2,可得a值;
(2)易判断直线l斜率不存在时不合题意,可设直线l:y=kx+
(k≠0),与椭圆方程联立消掉y得x的二次方程,则△>0,设M(x1,y1),N(x2,y2),MN的中点P(x0,y0),由|BN|=|BM|,则有BP⊥MN,所以kBP=
=-
,由韦达定理及中点坐标公式可得关于k的方程,解出k后验证是否满足△>0,从而可得直线l的方程;
| x2 |
| a2 |
| y2 |
| b2 |
|c-0+2
| ||
|
(2)易判断直线l斜率不存在时不合题意,可设直线l:y=kx+
| 3 |
| 2 |
| y0+1 |
| x0 |
| 1 |
| k |
解答:解 (1)设椭圆方程为
+
=1(a>b>0),则b=1.
设右焦点F(c,0)(c>0),则由条件得3=
,得c=
.
则a2=b2+c2=3,
∴椭圆方程为
+y2=1.
(2)若直线l斜率不存在时,直线l即为y轴,此时M,N为椭圆的上下顶点,|BN|=0,|BM|=2,不满足条件;
故可设直线l:y=kx+
(k≠0),与椭圆
+y2=1联立,消去y得:(1+3k2)x2+9kx+
=0.
由△=(9k)2-4(1+3k2)•
>0,得k2>
.
设M(x1,y1),N(x2,y2),MN的中点P(x0,y0),
由韦达定理得x1+x2=-
,而y1+y2=k(x1+x2)+3=-
+3.
则x0=
,y0=
由|BN|=|BM|,则有BP⊥MN,kBP=
=
=
=-
,
可求得k2=
,检验k2=
∈(
,+∞),所以k=±
,
所以直线l的方程为y=
x+
或y=-
x+
.
| x2 |
| a2 |
| y2 |
| b2 |
设右焦点F(c,0)(c>0),则由条件得3=
|c-0+2
| ||
|
| 2 |
则a2=b2+c2=3,
∴椭圆方程为
| x2 |
| 3 |
(2)若直线l斜率不存在时,直线l即为y轴,此时M,N为椭圆的上下顶点,|BN|=0,|BM|=2,不满足条件;
故可设直线l:y=kx+
| 3 |
| 2 |
| x2 |
| 3 |
| 15 |
| 4 |
由△=(9k)2-4(1+3k2)•
| 15 |
| 4 |
| 5 |
| 12 |
设M(x1,y1),N(x2,y2),MN的中点P(x0,y0),
由韦达定理得x1+x2=-
| 9k |
| 1+3k2 |
| 9k2 |
| 1+3k2 |
则x0=
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
由|BN|=|BM|,则有BP⊥MN,kBP=
| y0+1 |
| x0 |
| ||
|
-
| ||
-
|
| 1 |
| k |
可求得k2=
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 12 |
| ||
| 3 |
所以直线l的方程为y=
| ||
| 3 |
| 3 |
| 2 |
| ||
| 3 |
| 3 |
| 2 |
点评:本题考查直线方程、椭圆方程及其位置关系,考查分类讨论思想,判别式、韦达定理是解决该类题目常用知识,要熟练掌握,属中档题.

练习册系列答案
相关题目
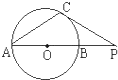 (2013•惠州一模)(几何证明选做题)
(2013•惠州一模)(几何证明选做题)