题目内容
11.设函数f(x)=x2-lnx.则零点个数为0个.分析 先求函数f(x)=x2-lnx的定义域,再求导可判断函数的单调性,从而可得f(x)≥f($\frac{\sqrt{2}}{2}$)=$\frac{1}{2}$-ln$\frac{\sqrt{2}}{2}$>0;从而确定答案.
解答 解:函数f(x)=x2-lnx的定义域为(0,+∞),
f′(x)=2x-$\frac{1}{x}$=$\frac{2{x}^{2}-1}{x}$;
故x∈(0,$\frac{\sqrt{2}}{2}$)时,f′(x)<0;
x∈($\frac{\sqrt{2}}{2}$,+∞)时,f′(x)>0;
故f(x)≥f($\frac{\sqrt{2}}{2}$)=$\frac{1}{2}$-ln$\frac{\sqrt{2}}{2}$>0;
故函数f(x)=x2-lnx没有零点;
故答案为:0.
点评 本题考查了导数的应用及函数的零点的判断,属于基础题.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
16.设等差数列{an}的前n项和Sn,若a1+a5+a8=a2+12,则S11=( )
| A. | 44 | B. | 66 | C. | 100 | D. | 132 |
3.等差数列{an}中,a1+a2=3,a3+a4=7,则a5+a6=( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
1.已知在函数f(x)=ex2+aex图象上点(1,f(1))处切线的斜率为e,则${∫}_{0}^{1}$f(x)dx=( )
| A. | 1-$\frac{2}{3}$ e | B. | 1+$\frac{2}{3}$e | C. | $\frac{2}{3}$e | D. | 1 |
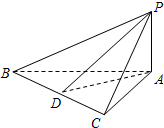 如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是8.
如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是8.